Updated July 25, 2023
Interpolation Formula (Table of Contents)
What is the Interpolation Formula?
The term “Interpolation” refers to the curve fitting technique that is used in the prediction of intermediate values and patterns on the basis of available historical data along with recent data points.
In other words, the interpolation technique can be used to predict the missing data points in-between the available data points.
The formula for interpolation is basically building a function for the unknown variable (y) based on the independent variable and at least two data points – (x1, y1) and (x2, y2). Mathematically, it is represented as,
Formula,
where,
- x = Independent Variable
- x1 = 1st Independent Variable
- x2 = 2nd Independent Variable
- y1 = Value of the Function at Value X1
- y2 = Value of The Function at Value x2
Example of Interpolation Formula (With Excel Template)
Let’s take an example to understand the calculation of the Interpolation Formula in a better manner.
Interpolation Formula – Example #1
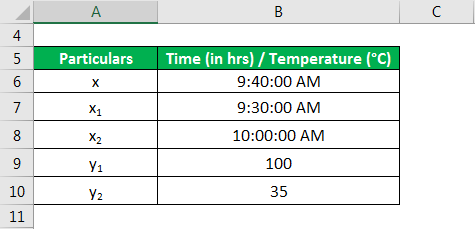
Let us take the example of a hot Rod to illustrate the concept of interpolation. Suppose that the Temperature of the Rod was 100°C at 9.30 A.M which gradually came down to 35°C at 10.00 A.M. Find the temperature of the Rod at 9.40 A.M based on the given information.
Solution:
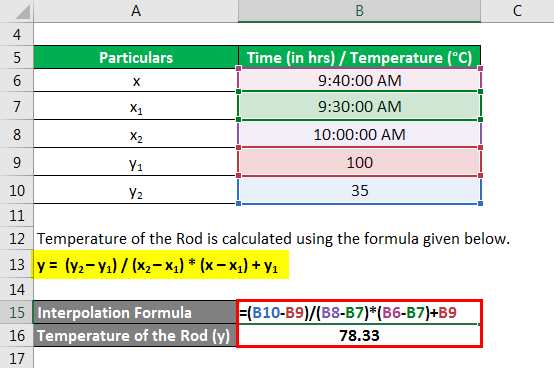
Temperature of the Rod(y) is calculated using the formula given below.
y = (y2 – y1) / (x2 – x1) * (x – x1) + y1
- Temperature of the rod (y) = (35 – 100) / (1000 – 930) * (940 – 930) + 100֯C
- Temperature of the rod (y) = 78.33֯C
Therefore, the temperature of the rod was 78.33֯C at 9.40 A.M.
Interpolation Formula – Example #2
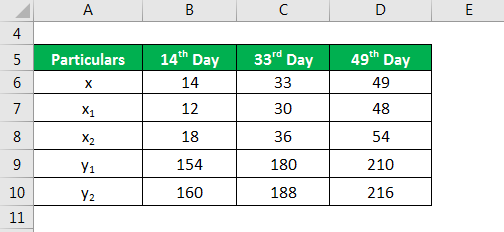
Let us take the curious case of John Doe who has been gaining significant weight in the last couple of months. As such, his doctor decided to monitor his weight and so started tracking his weight every 6 days for the last 60 days. The following information has been collected:
Solution:
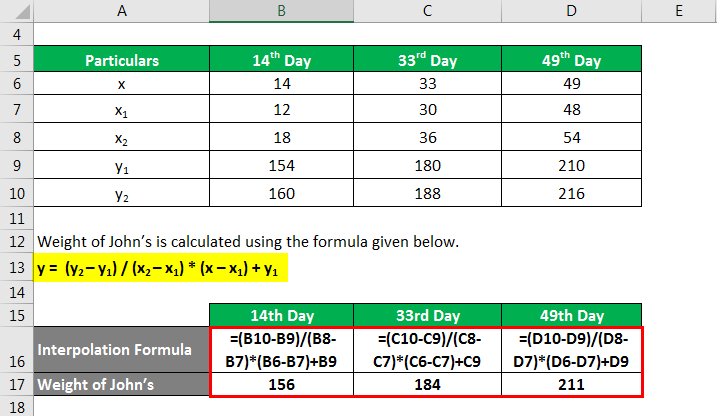
The weight of John′s is calculated using the formula given below.
y = (y2 – y1) / (x2 – x1) * (x – x1) + y1
On 14th day
- On 14th day = (160 – 154) / (18 – 12) * (14 – 12) + 154
- On 14th day = 156 lbs
On 33rd day
- On 33rd day = (188 – 180) / (36 – 30) * (33 – 30) + 180
- On 33rd day = 184 lbs
On 49th day
- On 49th day = (216 – 210) / (54 – 48) * (49 – 48) + 210
- On 49th day = 211 lbs
Therefore, John’s weight on 14th, 33rd and 49th day was 156 lbs, 184 lbs, and 211 lbs respectively.
Explanation
The formula for Interpolation can be calculated by using the following steps:
Step 1: Firstly, identify the independent and dependent variables for the function.
Step 2: Next, gather as many as possible historical and current data points in order to build a function. Make sure that there are at least two data points as it is the minimum data points required.
Step 3: Next, calculate the slope of the available data points by dividing the difference between the ordinates by that of the abscissas of the available data points.
Slope = (y2 – y1) / (x2 – x1)
Step 4: Finally, the function for interpolation can be derived by multiplying the slope (step 3) with the difference between the independent variable and the abscissa of any one data point and then adding the corresponding ordinate to the result as shown below.
y = (y2 – y1) / (x2 – x1) * (x – x1) + y1
Relevance and Use of Interpolation Formula
The importance of the interpolation technique can be gauzed from the fact that linear interpolation is believed to be used by Babylonian mathematicians and astronomers in the last three centuries BC, while the Greeks and Hipparchus used it in the 2nd century BC. One of the basic variants of interpolation is the linear interpolation technique which is commonly used by analysts in the field of mathematics, finance and computer programming. Please keep in mind that interpolation is a statistical and mathematical tool that is used to predict the intermediate values between two points.
Recommended Articles
This is a guide to Interpolation Formula. Here we discuss how to calculate the Interpolation Formula along with practical examples. We also provide a downloadable excel template. You may also look at the following articles to learn more –