Updated March 17, 2023

Introduction to Fibonacci Series in Python
Fibonacci series can be explained as a sequence of numbers where the numbers can be formed by adding the previous two numbers. It starts from 1 and can go upto a sequence of any finite set of numbers. It is 1, 1, 2, 3, 5, 8, 13, 21,..etc. As python is designed based on object-oriented concepts, multiple conditional statements can be used to design logic for the Fibonacci series. Three types of usual methods for implementing the Fibonacci series are ‘using python generators‘, ‘using recursion’, and ‘using for loop’.
For Example:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ..so on
So here 0+1 =1
1+1 = 2
1+2 = 3
2+3 = 5
3+5 = 8
5+8 = 13
8+ 13 = 21 and so on.
Looking at the above, one would have got a certain idea about what we are talking about.
However, In terms of mathematical rule, it can be written as:
![]()
Where nth number is the sum of the number at places (n-1) and (n-2). When it comes to implementing the Fibonacci series, there could be a number of coding languages through which it could be done.
However, Python is a widely used language nowadays. Let’s see the implementation of the Fibonacci series through Python. One should be aware of basic conditioning statements like the loop, if-else, while loop, etc., in Python before proceeding here. If not, it would be great if one can revise it and then take up the coming content. For demo purpose, I am using spyder, an IDE for the Python programming language. One can use any other IDE or Ipython notebooks as well for the execution of the Python programs.
Fibonacci Series in Python
Let’s see the implementation of Fibonacci number and Series considering 1st two elements of Fibonacci are 0 and 1:
However, you can tweak the function of Fibonacci as per your requirement but see the basics first and gradually move on to others.
Python Code for finding nth Fibonacci Number
Code 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2,m):
c = u + v
u = v
v = c
return vCode 2:

Output:
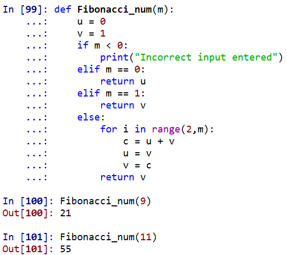
As one can see, the Fibonacci number at 9th place would be 21, and at 11th place would be 55.
- Here “fibonacci_num” is a function defined, which takes care of finding the Fibonacci number with the help of certain conditions. This function can be called by specifying any position.
Now let’s see how one can print series till the position mentioned:
Code:
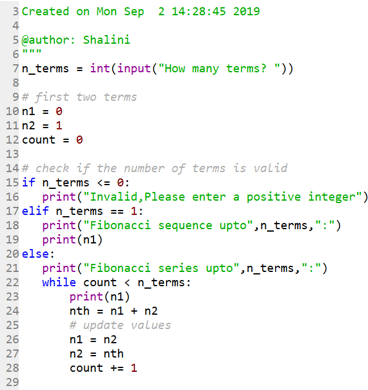
Output:
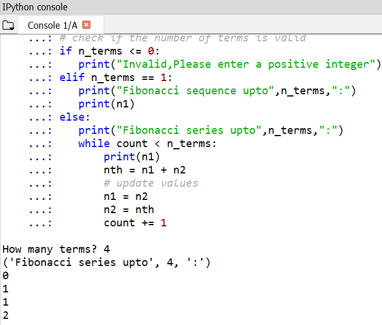
One can notice the start of Fibonacci numbers is defined as 0 and 1.
- If someone wants to define their own starting terms, that can also be done in the same way by tweaking n1 and n2. Here is the example for that:
Let’s say now we want our starting terms be: n1 = 3, n2 = 5
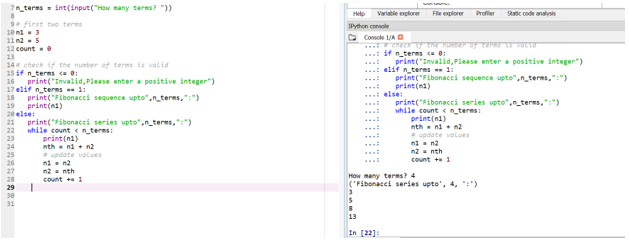
So here, your 4th term position (user input is taken) will be decided based on your starting terms.
Methods Through which Fibonacci Series can be Generated
Below are the three methods through which the Fibonacci series can be generated:
1. Through Generators
Code:
def fibo(num):
a,b = 0, 1
for i in xrange(0, num):
yield "{}:: {}".format(i + 1,a)
a, b = b, a + b
for item in fibo(10):
print itemOutput:
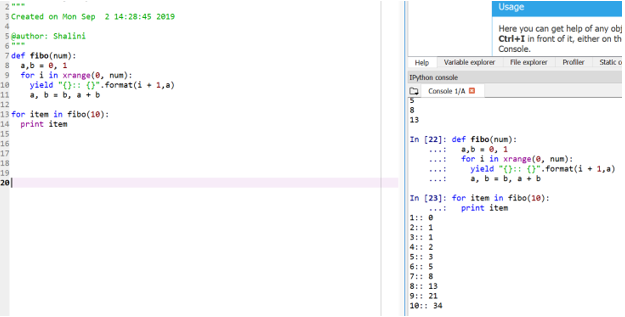
This method is referred to as “generator” because the function xrange is a generator of the numbers between 0 and num, and yield is the generator for formatted output.
Here is What xrange does for you:

Here Fibonacci series has been defined in the form of function, inside which for loop, xrange and yield function takes care of the output.
2. Through for loop
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + vOutput:

As one can see, a simple for loop has been used to print the Fibonacci series between 0 to 10. Inside for loop, new values have been assigned to the variables. U and v are the default initial values of Fibonacci that have been set to 0 and 1, respectively.
As for the loop progresses to run, the new u value is the old v value, whereas the new v value is the sum of old values of u and v. This continues till the end of range values.
3. Through Recursion
Code:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),Output:
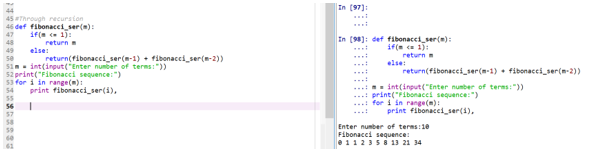
- The function “fibonacci_ser” is making the call to itself to print the Fibonacci series.
- And hence the method has got its name “recursion”.
Steps Followed here:
- Here the user has been asked to input the place till which the Fibonacci series needs to be printed.
- Number passes through the function “fibonacci_ser”.
- The condition gets checked if the length provided is less than 1 or not. If yes, the result is given immediately.
- However, if the length is greater than 1, recursive calls are made to “fibonacci_ser” with arguments having length lesser than 1 and 2, i.e. fibonacci_ser(m-1) and fibonacci_ser(m-2).
- Hence, recursion gives the desired output and print it.
- So, in short, We discussed Three ways for displaying the Fibonacci series.
- Through for loop, through generators and through recursion.
All Three Python Code’s Summarized
Below are the three python code:
1. Through Generators
Code:
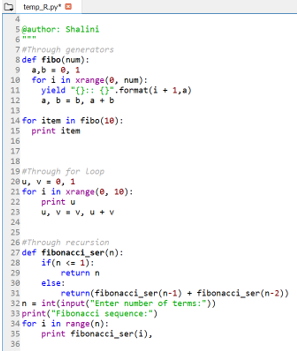
def fibo(num):
a,b = 0, 1
for i in xrange(0, num):
yield "{}:: {}".format(i + 1,a)
a, b = b, a + b
for item in fibo(10):
print item2. Through for loop
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v3. Through Recursion
Code:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),Summarized above are all procedures; one needs to practice to get a good grip on all.
Output:
Conclusion
Going through the above content of Fibonacci, one would have got a crystal clear understanding of Fibonacci numbers and series, specialized with python. Once one gets comfortable with the Fibonacci series’s logic, generating another series, working with other numbers, and various methods will now be a cakewalk for you. A logical approach is the only way to excel in this.
Recommended Articles
This is a guide to Fibonacci Series in Python. Here we discuss Fibonacci numbers and series, specialized with python, generating another series, working with other numbers, and various methods. You can also go through our other related articles to learn more –


