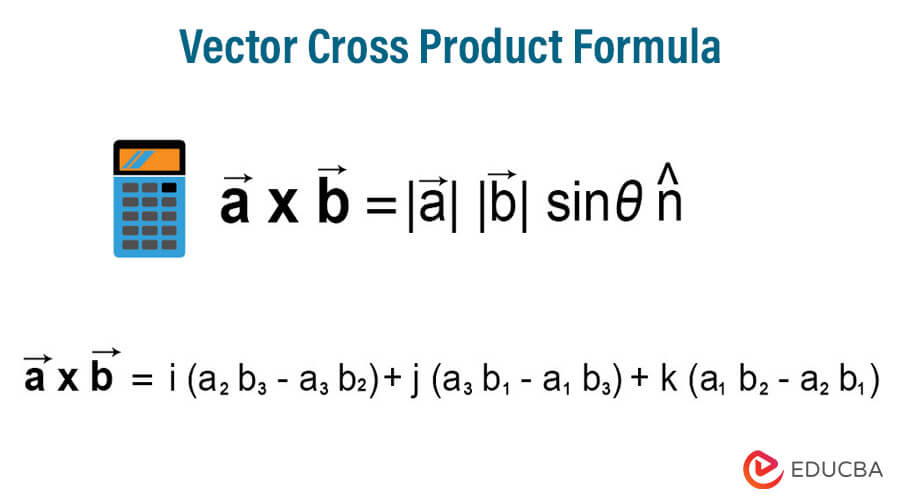Vector Cross Product Formula (Table of Contents)
What is the Vector Cross Product Formula?
In vector algebra and mathematics, the term “vector cross product” refers to the binary operations between vectors in the three-dimensional geometry. The cross product is signified by a cross sign “x” between the two vectors and the cross product operation results in another vector that is perpendicular to the plane containing the initial two vectors.
The formula for vector cross product can be derived by multiplying the absolute values of the two vectors and sine of the angle between the two vectors. Mathematically, let assume that a and b are two vectors, such that a = a1 i + a2 j + a3 k and b = b1 i + b2 j + b3 k, then vector cross product is represented as,
where θ = angle between a and b
|a| = √(a12 + a22 + a32)
|b| = √(b12 + b22 + b32)
n = Unit vector perpendicular to both a and b
Further, the vector cross product can also be expanded into its three-dimensional vector components, i.e. i, j and k, which are all perpendicular to each other. The formula for vector cross product is represented as,
Examples of Vector Cross Product Formula (With Excel Template)
Let’s take an example to understand the calculation of the Vector Cross Product in a better manner.
Vector Cross Product Formula – Example #1
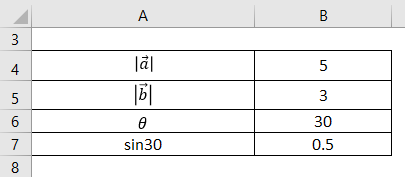
Let us take the example of two vectors a and b such that their scalar magnitude is |a| = 5 and |b| = 3, while the angle between the two vectors is 30 degrees. Calculate the vector cross product of the two vectors.
Solution:
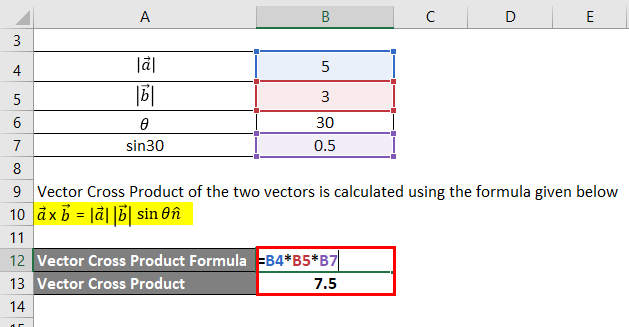
Vector Cross Product of the two vectors is calculated using the formula given below
a x b = |a| |b| sinθn
- a x b = 5 * 3 * sin30n
- a x b = 7.5 n
Therefore, the vector cross product of the two vectors is 7.5.
Vector Cross Product Formula – Example #2
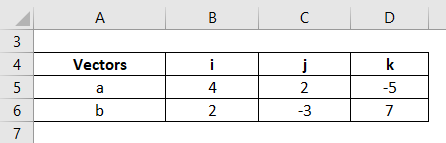
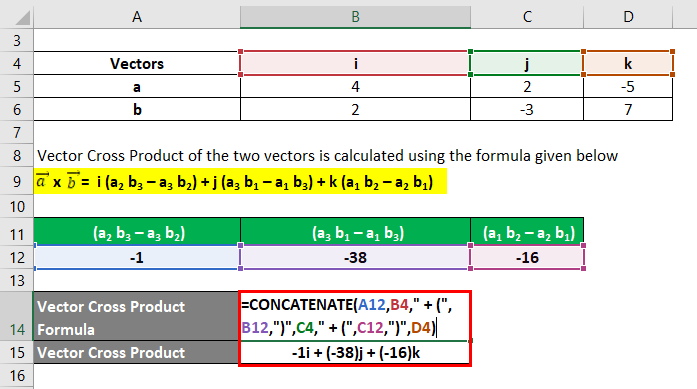
Let us take the example of two vectors a (4, 2, -5) and b (2, -3, 7) such that a = 4i + 2j – 5k and b= 2i – 3j + 7k. Calculate the vector cross product of the two vectors.
Solution:
Vector Cross Product of the two vectors is calculated using the formula given below
a x b = i (a2 b3 – a3 b2) + j (a3 b1 – a1 b3) + k (a1 b2 – a2 b1)
- a x b = i {2 * 7 – (-5) * (-3)} + j {(-5) * 2 – 4 * 7} + k {4 * (-3) – 2 * 2}
- a x b = -i + (– 38j) + (– 16k)
Therefore, the vector cross product of the two vectors (4, 2, -5) and (2, -3, 7) is (-1, -38, -16).
Vector Cross Product Formula – Example #3
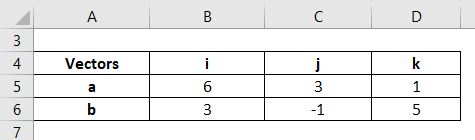
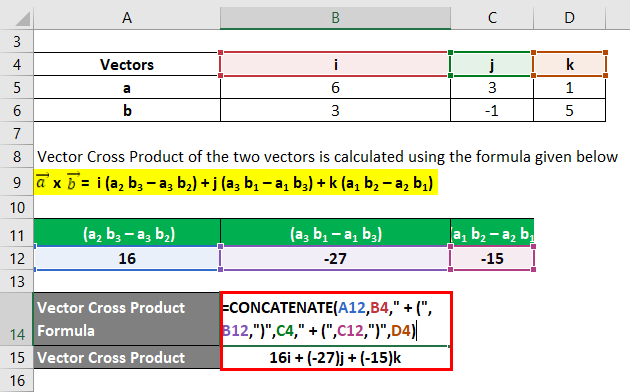
Let us take the example of a parallelogram whose adjacent sides are defined by the two vectors a (6, 3, 1) and b (3, -1, 5) such that a = 6i + 3j + 1k and b = 3i – 1j + 5k. Calculate the area of the parallelogram.
Solution:
Now, the vector cross product of the two vectors can be calculated using above formula as,
a x b = i (a2 b3 – a3 b2) + j (a3 b1 – a1 b3) + k (a1 b2 – a2 b1)
- a x b = i {3 * 5 – 1 * (-1)} + j {1 * 3 – 6 * 5} + k {6 * (-1) – 3 * 3}
- a x b = 16i + (– 27j) + (– 15k)
Now, the area of the parallelogram can be derived by computing the magnitude of the vector cross product as,
- |a x b| = √[(16)2 + (-27)2 + (-15)2]
- |a x b|= 34.79
Therefore, the area of the parallelogram is 34.79.
Explanation
The formula for vector cross product can be derived by using the following steps:
Step 1: Firstly, determine the first vector a and its vector components.
Step 2: Next, determine the second vector b and its vector components.
Step 3: Next, determine the angle between the plane of the two vectors, which is denoted by θ.
Step 4: Finally, the formula for vector cross product between vector a and b can be derived by multiplying the absolute values of the a and b which is then multiplied with the sine of the angle (step 3) between the two vectors as shown below.
a x b = |a| |b| sinθn
Relevance and Uses of Vector Cross Product Formula
The concept of vector cross product has diverse applications in the field of engineering, mathematics, computational geometry, physics, computer programming, etc. The underlying concept helps us in determining not only the magnitude of the scalar component of the product of two vectors, but it also provides the direction of the resultant. Further, it is also used to determine the angle between the planes of the two vectors. The concept and applications of vector cross products can be very complex and interesting.
Recommended Articles
This is a guide to the Vector Cross Product Formula. Here we discuss how to calculate Vector Cross Product along with practical examples and downloadable excel template. You may also look at the following articles to learn more –