Doubling Time Formula (Table of Contents)
What is Doubling Time Formula?
Doubling time, as its name suggests is the time taken or the length of time in which your investment will become double in size at some particular rate of interest. This concept is also very commonly known as Rule of 70 because doubling time can be approx. calculated by dividing 70 with the interest rate. This will also lead to the almost the same value as doubling formula. This concept is very common in comparing investments which have different interest rates and helps us in understanding how quickly that investment grows.
This tool is widely used by analysts and investors for evaluating various investments like mutual fund returns, portfolio returns etc. and can take appropriate decision to achieve the target. For example, if you are an investor and upon doubling time calculation, you know that your investment will be doubled in almost 20 years. Now you can use this time to reduce, and your investment will be close to 15 years, you need to increase the rate of return of your investment. For that, you can allocate changes to the portfolio to achieve that rate.
The formula for Doubling Time –
There are 2 ways by which we can find doubling time and both will yield almost the same answer:
Where:
- Ln – Natural Log
- r – Interest Rate
In this formula, use the absolute value of r and not the decimal value. For example: if r is given like 5%, we will use 5 and not 0.05.
Examples of Doubling Time Formula (With Excel Template)
Let’s take an example to understand the calculation of Doubling Time formula in a better manner.
Doubling Time Formula – Example #1
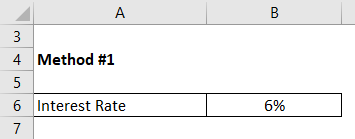
Find the time it will take to doubling your money if you can get a constant growth rate of 6%.
4.9 (3,296 ratings)
View Course
Solution:
Doubling Time is calculated using the formula given below
Doubling Time = Ln (2) / Ln (1+r)
In this formula, use the absolute value of r and not the decimal value.
- Doubling Time = Ln (2) / Ln (1 + 6%)
- Doubling Time = 11.90 years
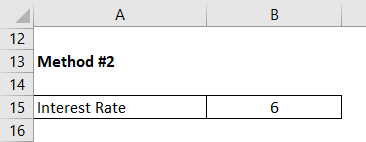
In Method 2, use the absolute value of r and not the decimal value.
Doubling Time is calculated using the formula given below
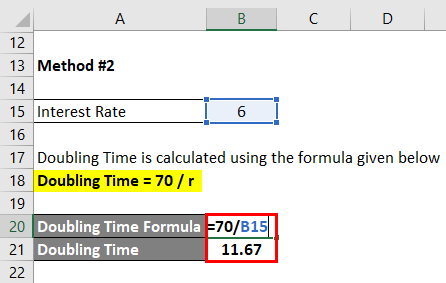
Doubling Time = 70 / r
- Doubling Time = 70 / 6
- Doubling Time = 11.67 years
So if you see, both the formulas resulting in approx. same answer and if we round off the results, it will take us around 12 years to double the money given a 6% rate.
Doubling Time Formula – Example #2
Let say bank A is offering you a 10% constant interest rate if you invest your funds with them and bank B is offering 12% constant growth rate. You want to see how fast your investment will grow and how much time it will take to double your funds.
Solution:
Doubling Time is calculated using the formula given below
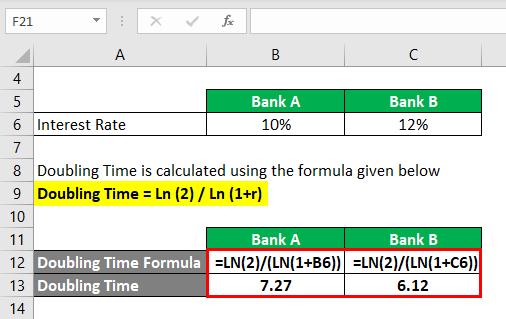
Doubling Time = Ln (2) / Ln (1+r)
For Bank A:
- Doubling Time = Ln (2) / Ln (1 + 10%)
- Doubling Time = 7.27 years
For Bank B:
- Doubling Time = Ln (2) / Ln (1 + 12%)
- Doubling Time = 6.12 years
So if you choose investment in A, your funds will be doubled in 7.27 years but B will double your more in 6.11 years.
Explanation
Although doubling time or rule of 70 gives us the estimate of time in which we can double our investment, the major assumption here is the constant growth rate. So if it is not constant, our estimate will be prone to errors and will not accurate. This happens in real life since interest rates do not remain constant and vary with time. So this concept is more of a theoretical concept and has less relevance in practical life. Another thing to keep in mind the interest rate in the doubling time in the rate per period. So if the compounding is happening monthly, we need to convert that rate into the monthly rate and then calculate the doubling time. But nevertheless, it is an important tool and helps us to understand the compounding effect and also very helpful in quickly working around to see the time it will take to double your money.
Relevance and Uses of Doubling Time Formula
Since doubling formula will help you in determining the time to double your investment, it also helps you to make decisions based on that. For example, if you know that given the market rate, you will not be able to double your money in the time which you want, you need to try to increase the growth rate by taking more risk and change your portfolio allocation. But there are some limitations also which make the use of doubling formula very limited. So, in nutshell, This tool can only be used where the growth rate is expected to be steady and constant throughout the investment period and if that rate is expected to vary, there is no point in using this formula.
Doubling Time Formula Calculator
You can use the following Doubling Time Calculator
| r | |
| Doubling Time Formula | |
| Doubling Time Formula | = |
| |||||
| = |
|
Recommended Articles
This has been a guide to Doubling Time Formula. Here we discuss How to Calculate Doubling Time along with practical examples. We also provide Doubling Time Calculator with downloadable excel template. You may also look at the following articles to learn more –
