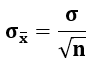Updated July 29, 2023
Central Limit Theorem Formula (Table of Contents)
- Central Limit Theorem Formula
- Examples of Central Limit Theorem Formula (With Excel Template)
- Central Limit Theorem Formula Calculator
Central Limit Theorem Formula
The central limit theorem formula is widely used in probability distribution and sampling techniques. The central limit theorem states that as the sample size gets larger and larger, the sample approaches a normal distribution.
No matter the population distribution shape, the fact essentially holds true as the sample size is over 30 data points. The central limit theorem essentially has the following characteristics:-
- Mean of Sample is the same as the mean of the population.
- The standard deviation calculated is the same as the population’s standard deviation divided by the sample size’s square root.
A formula for Central Limit Theorem is as below:
Where,
- σ = Population Standard Deviation
- σx¯ = Sample Standard Deviation
- n = Sample size
Examples of Central Limit Theorem Formula (With Excel Template)
Let’s take an example to understand the calculation in a better manner.
Example #1
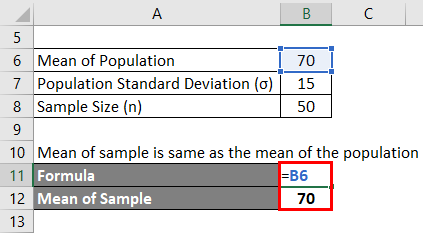
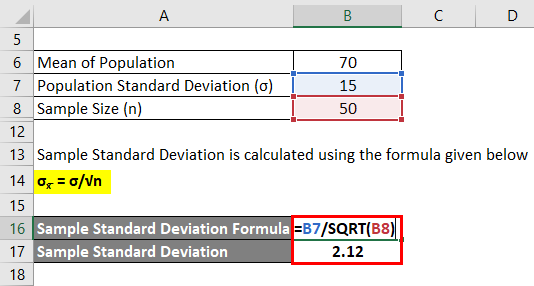
In a country in the middle east region, the recorded weights of the male population follow a normal distribution. The mean and the standard deviations are 70 kg and 15 kg, respectively. If a person is eager to find the record of 50 males in the population, then what would mean and the standard deviation of the chosen sample?
Solution:
Mean of Sample is the same as the mean of the population.
The mean of the population is 70 since the sample size > 30.
The formula to calculate Sample Standard Deviation is as below:
σx= σ/√n
- Sample Standard Deviation = 15 / √50
- Sample Standard Deviation = 2.12
Example #2
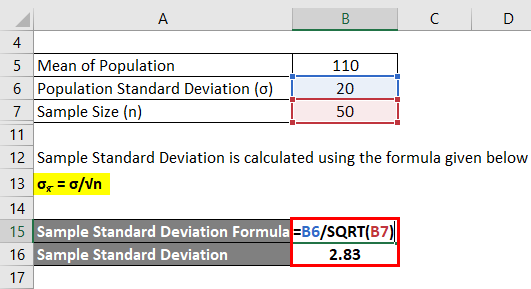
A certain group of people gives their annual pension benefit of Rs. 110 per week with a standard deviation of Rs. 20 per week. If a random sample of 50 people is taken, what will be the mean and the standard deviation of the pension benefits received?
Solution:
Mean of Sample is the same as the mean of the population.
The mean of the population is 110 since the sample size > 30.
σx= σ/√n
- Sample Standard Deviation = 20 / √50
- Sample Standard Deviation = 2.83
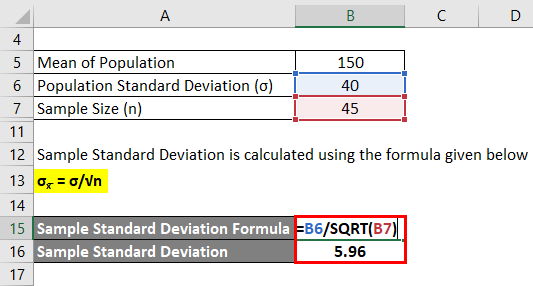
Example #3
A certain group of people gives their annual hardship allowance benefit of Rs. 150 per month with a standard deviation of Rs. 40 per month. If a random sample of 45 people is taken, what will be the mean and the standard deviation of the pension benefits received?
Solution:
Mean of Sample is the same as the mean of the population.
The mean of the population is 150 since the sample size > 30.
σx= σ/√n
- Sample Standard Deviation = 40 / √45
- Sample Standard Deviation = 5.96
Explanation
The formula of the central limit theorem states that with an infinite number of successive random samples taken in the population, the sampling distribution of the selected random variables will become approximately normally distributed in nature as the sample size gets larger and larger in size.
Relevance and Uses of Central Limit Theorem
- The central limit theorem is widely used in sampling, probability distribution, and statistical analysis where a large sample of data is considered and needs to be analyzed in detail.
- The central limit theorem is also used in finance to analyze stocks and indexes, which simplifies many analysis procedures as generally, and most of the time, you will have a sample size greater than 50.
- Investors of all types rely on the CLT to analyze stock returns, construct portfolios and manage risk.
- A central limit theorem is also used in binomial probability, which plays an active role in analyzing statistical data in detail.
Calculator
You can use the following Central Limit Theorem Calculator
| σ | |
| √n | |
| Sample Standard Deviation Formula
| |
| Sample Standard Deviation Formula | = |
|
|
Recommended Articles
This has been a guide to Central Limit Theorem Formula. Here we discuss how to calculate Central Limit Theorem along with practical examples. We also provide the Central Limit Theorem calculator with a downloadable Excel template. You may also look at the following articles to learn more –