Updated July 1, 2023
Introduction to Bisection Method Matlab
Bisection method is used to find the root of equations in mathematics and numerical problems. This method can be used to find the root of a polynomial equation, given that the roots must lie in the interval defined by [a, b], and the function must be continuous in this interval. The bisection method requires 2 guesses initially and so is referred to as the ‘close bracket’ type. Compared with other root-finding methods, this method is relatively slow as it converges in a linear, steady, and slow manner.
We do not have a pre-defined bisection method in MATLAB, so we create one to get the roots using this method.
How to create the Bisection method in MATLAB?
Let us now understand the syntax to create the bisection method in MATLAB:
Syntax
1. Z = input (‘Enter the input function and set right-hand side equal to zero:,’ ‘s’);
[Asking the user to enter the input function]2. f = inline (Z);
[Calling inline command to create the function in MATLAB using the above input equation]initialValue = input ('Enter the initial value for guess interval:');
- [Asking user to enter ‘Initial value,’ which is used as the first value for 1st iteration]
endValue = input ('Enter the last value for guess interval:');
- [Asking user to enter ‘End value’, which is used as the last value for 1st iteration]
allowedError = input ('Enter the error allowed:');
- [Asking the user to enter tolerable error]
Code:
if f (endValue) * f (initialValue) < 0
else
fprintf('The guess entered is incorrect. Please enter the new guess\n');
initialValue = input ('Enter the initial value for guess interval:\n') ;
endValue = input ('Enter the last value for guess interval:\n');
end
for I = 2 : 500
iter1 = (endValue + initialValue) / 2;
if f (endValue) * f (iter1) < 0
initialValue = iter1;
else
endValue = iter1;
end
if f (initialValue) * f (iter1) < 0
endValue = iter1;
else
initialValue = iter1;
end
iterN (1) = 0;
iterN (i) = iter1;
if abs ((iterN (i) – iterN (i-1)) / iterN (i)) <allowedError, break, end
end
outStr = ['Required root for the input equation is: ', num2str(iter1), '']
1. Mid-point for the range [ initialValue, endValue ] is calculated. We have defined the midpoint as iter1, which is defined as:
iter1 = (initialValue + endValue) / 2
2. The value of the input function is calculated at ‘iter1’, giving the following scenarios:
- If f (iter1) = 0; iter1 will be the required root
- If f (endValue) * f (iter1)> 0, i.e, the product f (endValue) * f (iter1) is positive, then the root of the input function will lie between the range [firstValue, iter1].
- If f (endValue) * f (iter1)< 0; i.e, the product f (endValue) * f (iter1) is negative, then the root of the input function will lie between the range [ endValue, iter1]]
Example to Implement Bisection Method Matlab
Below are the examples mentioned:
Example #1
In this example, we will take a polynomial function of degree 2 and will find its roots using the bisection method. We will use the code above and will pass the inputs as asked. For our first example, we will input the following values:
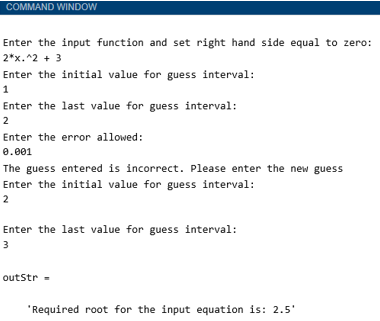
- Pass the input function as 2*x.^2 + 3
- Pass the firstValue as 1
- Pass the endValue as 2
- Pass the allowed error as 0.001
- If the root does not lie between 1 & 2, then the code will again ask for firstValue and endValue
- Pass the firstValue as 2 and endValue as 3 this time
Output:
As we can see in the output, we have obtained the root of our input function as 2.5.
Example #2
In this example, we will take a polynomial function of degree 3 and will find its roots using the bisection method. We will use the code above and will pass the inputs as asked. For this example, we will input the following values:
- Pass the input function as 3*x.^3 + 2*x.^2
- Pass the firstValue as 1
- Pass the endValue as 3
- Pass the allowed error as 0.001
- The code will again ask for firstValue and endValue
- Pass the firstValue as 2 and endValue as 3 this time
Output:
As we can see in the output, we have obtained the root of our input function as 2.5.
Next, let us see an example where we are not asked for the guess values the second time
Example #3
In this example, we will take a polynomial function of degree 2 and will find its roots using the bisection method. We will use the code above and will pass the inputs as asked. For this example, we will input the following values:
- Pass the input function as x.^2 – 3
- Pass the firstValue as 1
- Pass the endValue as 2
- Pass the allowed error as 0.001
Output:
As we can see in the output, we have obtained the root of our input function as 1.7344, after we input our guess values for the first time.
Conclusion
The bisection method is used to find the root of any polynomial function. As there is no direct function for the bisection rule in MATLAB, we define the code or logic for it manually.
Recommended Articles
This is a guide to Bisection Method Matlab. Here we discuss an introduction to Bisection Method Matlab, syntax, parameters, and examples for better understanding. You can also go through our other related articles to learn more –