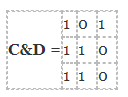Updated March 23, 2023
Introduction to Matlab AND Operator
In this article, we will see an outline on Matlab AND Operator. Logical operators control the execution of program flow according to conditions that result from a set of expressions. They are very easy to use and to understand the flow of any program. They can be used to check the number of zeroes in an array or any conditional statement if it matches a particular requirement. Three types of logical operators are used in any programming language i.e. OR (C|D), AND (C & D), NOT(~C). They result in Boolean values i.e. either True/False or 0/1. If a particular condition is false, then it results in 0 else 1.
Working of Matlab AND Operator
In Matlab, logical operators function in a similar way as in other programming languages. Logical AND operator results in 0/1 or True/False based on the type of signals that we provide to the input. They are denoted by & operator (C&D). Please find the below truth table to see the output for different combinations of input signals.
Truth Table:
|
Input 1 (C) |
Input 2
(D) |
Output (C&D) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
According to the above table, when any of the operands i.e. C and D are 0 or false the resulting output is false or 0. Similarly, if the operands are true or 1 then the resulting output is true or 1. In Matlab, we can use logical AND operator by defining as C&D. It can also be defined as ‘ and (C, D)’ but this syntax is used rarely because of operator overloading issues. So, it’s better to define the operator using C&D format in Matlab. Please find the below example to understand how AND operator works:
Examples of Matlab AND Operator
Below are the examples of Matlab AND Operator:
Example #1
G = [0,1,0,0,0,1]
H= [ 0,1,0,0,1,1]
Output:
In the above example, the first and second array consists of an array of 0 and 1. If we use AND operator between two arrays then, if both the elements are true in the above two arrays, it results in True or 1. The second and sixth element of both arrays has 1 so the resulting output is 1 while rest other combinations have 0, so the resulting output is 0. The inputs or operands can be vectors, scalar, matrix or multi-dimensional array. They can be of the same size or a different size.
Like Logical OR operator, logical AND operator can also be used in the short-circuiting principle. They have a different working principle as compared to normal & operator in Matlab. They are defined by the && operator. If there are two expressions, then the second part of the defined expression is not evaluated if the first part of the defined expression is false or 0. The resulting output from the expressions is always scalar is nature if we are using short-circuiting principles. In short, the second part of the defined expression always depends on the first part whether we use logical && or || operator in Matlab defining its short-circuiting nature.
Example #2
C = 0
D= 18
Y= (C==1) && (C*D<0)
Output:
In the above expression, it evaluates the first part of the defined expression which is not true since we have assigned the values of C as 0. So, according to the short-circuiting behavior of AND operator in Matlab, if the first part of the given expression is false then it doesn’t evaluate the second part of the defined expression and it results in logical 0 or false evaluating only the first expression. The output is 0 which is scalar in nature. We should be careful while using the & and && operator in Matlab because both will give you different outputs.
Logical AND operator is also used to determine the condition satisfying a particular criterion by resulting in 0 and 1. If the result is 1 then it matches a particular condition else the result is 0. Please find the below example demonstrating the above part:
Example #3
C = [3, 0 ,5 ; 8, 1 ,0 ; 4, 3, 0]
| C = | 3 | 0 | 5 |
| 8 | 1 | 0 | |
| 4 | 3 | 0 |
D= [8, 0, 6; 2, 1, 0; 5, 7, 0]
| D = | 8 | 0 | 6 |
| 2 | 1 | 0 | |
| 5 | 7 | 0 |
Output:
In the above two matrices, it checks both the elements of the matrix and results in 0 and 1 based on the values. If the values of the matrices are not zero, then then it results in 1 and 0 if both the elements are 0.
Conclusion
Logical operators form a very important part in many programming languages like Java, Python, C, etc. So, it’s important to understand the working of these operators to use the program while executing any code. We should be aware of the business requirements and use the operators as needed. For example, && and && or || and | operator will give different outputs when used in an expression.
Recommended Articles
This is a guide to Matlab AND Operator. Here we discuss the Introduction to Matlab AND Operator with practical examples and different combinations of input signals. You can also go through our suggested articles to learn more –