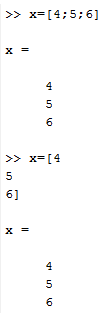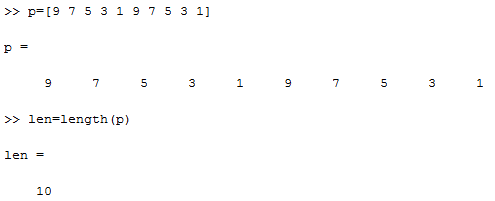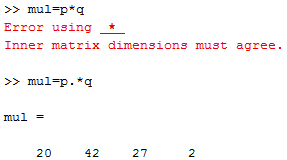Updated March 21, 2023

Introduction to Vectors in Matlab
A vector is an enclosed set of elements. In Matlab, we can create vectors by using square brackets. Vectors are one of the illustrations of arrays (one-dimensional array). it can be represented in two ways row vector and column vector.
Row Vector
It is horizontal set of elements. It is represented within square brackets. Each element is separated by comma or space.
X = [ 4 7 8 ] or X = [ 4 , 7 , 8 ]
Column Vector
It is a vertical set of elements. It is also represented within square brackets. There are two ways to create column vectors first is by separating each element by a semicolon and another way is writing each element on the next row in the command window.
X = [ 4 ; 6 ; 7 ] or
X = [ 4
6
7 ]
Vector Operations
Vector operators are broadly classified into two categories.
1. Arithmetic Operation
Let us consider two vectors x and y with values x = [ 1 4 5 3 ] and y = [ 5 3 2 1 ] we can perform various operations on these two vectors x and y.
a. Multiplication: This function is used to multiply by any arithmetic value to the entire vector.
For Example:
mul = 3 * x
mul = 3* [ 1 4 5 3 ]
mul = [ 3 12 15 9 ]
Syntax: variable name = arithmetic constant * vector name
b. Trigonometric Function: We can apply any trigonometric function on vector-like sin, cos, tan, cosec, sec, etc.
Example tri = cos ( x )
Answer is : 0.54 – 0.65 0.28 -0.99
Syntax: variable name = trigonometric function name ( vector name )
Sum: This shows a total of (addition of ) entire elements in one vector.
Example
x = [ 1 4 5 3 ]
Total = sum ( x )
Output is total = 13
Syntax: variable name = = sum ( vector name )
c. Length: It shows length of particular vector , let us one vector p = [ 9 7 5 3 1 9 7 5 3 1 ]
Example
p = [ 9 7 5 3 1 9 7 5 3 1 ]
Len = length ( p )
Output is Len = 10
d. Addition of Vectors: The addition of two or multiple vectors is a simple operation in Matlab, let us consider two vectors p and q.
P = [ 4 6 3 2 ] and q = [ 5 7 9 1 ]
Add = p + q
Output is Add = [ 9 13 12 3 ]
Syntax: vector name operator ( + ) vector name
Similarly, we can do subtraction operation like sub = p – q
e. Multiplication of Vectors: If we want to do multiplication of two vectors then a simple multiplication operator ( * ) will not work. Therefore we need to add a dot operator ( ‘ . ‘ ) with a multiplication operator.
Example:
P = [ 4 6 3 2 ] and q = [ 5 7 9 1 ]
mul = p . * q
output is mul = [ 20 42 27 2 ]
Syntax: variable name = vector name dot operator multiplication operator vector name
Suppose I want to find out the square of one particular vector or I want to multiply the vector by that vector only.
Then syntax will be squr = x. ^ 2
2. Relational Operation
a. Equal to the operator: this operator compares each n every element from two vectors and gives output is zero and one form.
Example
m = [ 2 5 8 ]
And n = [ 5 5 3 ]
As we know there are three elements in vector m and vector n,
m == n
The above statement will give output as 0 1 0, which means first no is not equal, the second number is equal and the third no is not equal. O represents false and 1 represents true.
b. Less than operator (<): Less than the operator represents by symbol ‘ <’. we can compare a given matrix with any arithmetic constant or with any other vector.
Example
m = [ 3 2 4 ]
n = [ 1 1 1]
m < n
the output will be 0 0 0, which means all numbers are greater than vector n.
and if m < 10
then the output will be 1 1 1, which means all numbers are less than 10.
c. Greater than operator (>): Greater than the operator represents by the symbol ( ‘ > ’). We can compare a given matrix with any arithmetic constant or with any other vector.
Example:
M = [ 3 2 4 ]
N = [ 1 1 1 ]
m > n
Output will be 1 1 1 ,that means all values are greater than values of vector n.
Conclusion – Vectors in Matlab
In Matlab, we can create different types of vectors where we can perform various operations like addition, subtraction, multiplication, square, square root, power, scaling, vector multiplication, dot product, etc.
Recommended Articles
This is a guide to Vectors in Matlab. Here we discuss the types of vector operation which include arithmetic and relational Operation along with some Examples. You may also look at the following articles to learn more –