Binomial Distribution Formula (Table of Contents)
What is Binomial Distribution Formula?
The binomial distribution is the probability distribution formula that summarizes the likelihood of an event occurs either A win, B loses or vice-versa under given set parameters or assumptions. However, there is an underlying assumption of the binomial distribution where there is only one outcome is possible for each trial, either success or loss. And each trial in itself is mutually exclusive from another one.
Suppose, if we have defined one outcome out of two is defined as a success, then the probability of x successes out of N trials can be computed as:
Where p is the probability of success on one trial.
Examples of Binomial Distribution Formula
Let’s take an example to understand the calculation of Binomial Distribution in a better manner.
Binomial Distribution Formula – Example #1
A coin is flipped 10 times. Calculate the probability of getting 5 heads using a Binomial distribution formula.
Solution:
Probability is calculated using the binomial distribution formula as given below.
P(X) = (n! / (x! * (n – x)!)) * px * (1 – p)(n-x)
- P(x=5) = (10! / (5! * (10 – 5)!)) * (0.5)^5 * (1 – 0.5)^(10 – 5)
- P(x=5) = (10! / (5! * 5!)) * (0.5)^5 * (0.5)^5
- P(x=5) = 0.2461
The probability of getting exactly 5 successes is 0.2461
Binomial Distribution Formula – Example #2
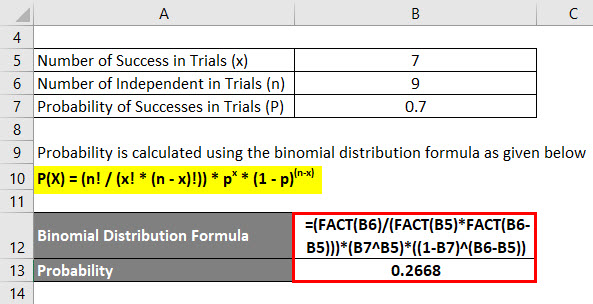
In a study, it is found that 70% of people who purchase pet insurance are mostly women. If we randomly select 9 pet insurance owners. What is the probability, out of the 7 will be women?
Solution:
Probability is calculated using the binomial distribution formula as given below.
P(X) = (n! / (x! * (n – x)!)) * px * (1 – p)(n-x)
- P(x=7) = (9! / (7! * (9 – 7)!)) * (0.7)^7 * (1 – 0.7)^(9 – 7)
- P(x=7) = (9! / (7! * 2!)) * (0.7)^7 * (0.3)^2
- P(x=7) = 0.2668
Binomial Distribution Formula – Example #3
Last year in the survey of Autocar India, it was found that 70% of buyers of sports cars are men. If 10 sports car owners are randomly selected. What is the probability, out of the 6 will be men?
Solution:
Probability is calculated using the binomial distribution formula as given below.
P(X) = (n! / (x! * (n – x)!)) * px * (1 – p)(n-x)
- P(x=5) = (10! / (6! * (10 – 6)!)) * (0.7)^6 * (1 – 0.7)^(10 – 6)
- P(x=5) = (10! / (6! * 4!)) * (0.7)^6 * (0.3)^4
- P(x=5) = 0.2001
Explanation
A binomial distribution basically depends much more on the number of trials or observations are done. While each trial defines its own probability of outcome value or, in other words. A binomial random variable defines as a successful outcome of x in n number of the repeated trial of a binomial experiment. While a binomial random variable’s probability distribution is also known as a binomial distribution.
If we take an example, when we toss a coin, the probability of obtaining a head is 0.5 of 50% out of 100%. If we perform 100 trials. The expected value of obtaining heads is 50(100 x 0.5). The binomial distribution is a statistical term to predict the outcome of an event to occur, like what is the probability of a sportsman to win in the competition.
There are certain steps and rules to meet the specific criteria of Binomial Distribution models in order to use the formula.
Step 1: Fixed Trials
In this course of action, there is a certain set of a fixed number of trials which can’t be altered in the course of the whole process. The number of trials in the binomial probability formula is represented by the letter “n”. In our case, flips a coin, free throws, wheel spins are the fixed number of trials.
Step 2: Independent Trials
Independent Trial is another condition of a binomial probability in which trials are independent of each other where the outcome of one trial doesn’t impact much more on the subsequent trials.
If we take an example where independent trials, maybe tossing a coin or rolling dice, is independent of the subsequent events.
Step 3: Fixed Probability of Success
In this type of distribution, the probability of getting success remain the same for all trials. For example, if we toss a coin, the probability of an outcome of every event, either head or tail, is 0.5 since there are two possible outcomes.
Step 4: Two Mutually exclusive Outcomes
In this distribution, there are only two types of mutually exclusive outcomes that exist, either success or failure. Where success has been defined in a positive term. The purpose of the trial is to validate what we have defined as a success. Either it is positive or negative.
Relevance and Uses of Binomial Distribution Formula
The binomial distribution model is the most important probability model; it is required when there are two possible outcomes expected. It came into existence when there were more than two distinct outcomes. In that case, a multinomial probability is more appropriate. But here, our major concern is more on the situation where the outcome is dichotomous.
The use of the binomial distribution requires three models:
- Each outcome of the process results in the one or two outcomes, either success or failure.
- The outcome of each process results in the same probability.
- Each outcome is mutually exclusive to the other of the process.
Binomial Distribution Formula Calculator
You can use the following Binomial Distribution Calculator.
| n | |
| p | |
| x | |
| Binomial Distribution Formula | |
| Binomial Distribution Formula = | [n ! / x ! * (n - x) !] * px * (1 - p)n - x | |
| [0! / 0! * (0 - 0)!] * 00 * (1 -0)0-0 = | 0 |
Binomial Distribution Formula in Excel (With Excel Template)
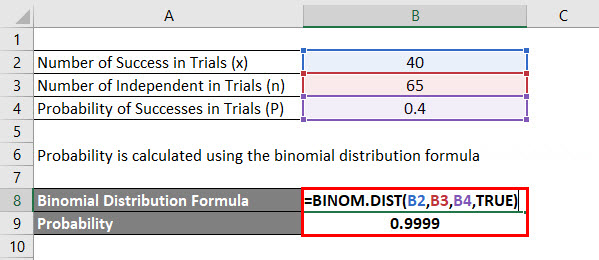
Here we will do another example of the Binomial Distribution in Excel. It is very easy and simple.
Calculate the Binomial Distribution in Excel using function BINOM.DIST.
Below is the Syntax of Binomial Distribution formula in Excel.
Where the Binomial distribution uses the following argument:
- Number_s: Defines the number of success in the trial.
- Trials: Number of independent trials.
- Probabiity_s: Success probability in each trial.
- Cumulative: Allows to pick logical value either True or False.
Probability is calculated using the binomial distribution formula is calculated as:
Recommended Articles
This has been a guide to Binomial Distribution Formula. Here we discuss how to calculate Binomial Distribution along with practical examples. We also provide a Binomial Distribution calculator with a downloadable excel template. You may also look at the following articles to learn more –
