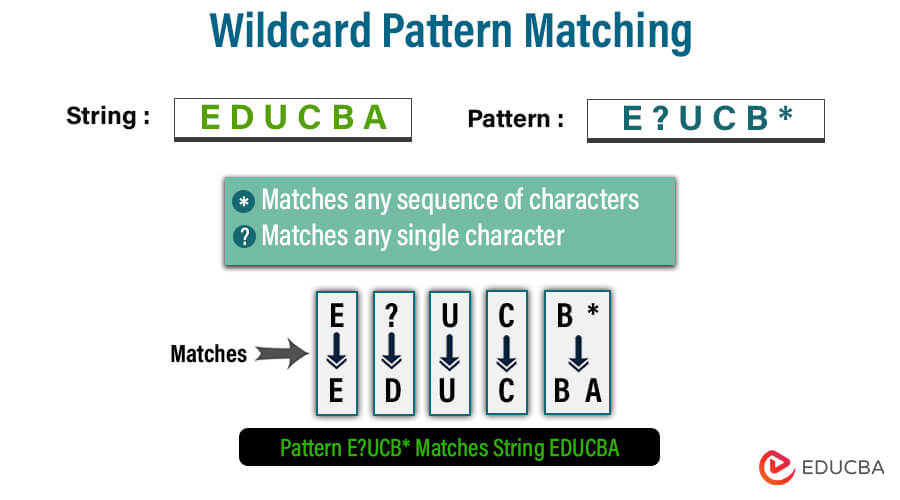
What is Wildcard
Wildcards are characters used in various contexts, particularly in text processing and pattern matching, representing one or more unknown or variable characters within a string. They allow for flexible and efficient searching and matching of patterns in text. Some commonly used wildcard characters are:
- “*” (Asterisk):
- Matches zero or more characters.
- For example, the pattern “ab*c” would match strings like “abc,” “abbc,” and “abbbc.”
- “?” (Question Mark):
- Matches exactly one occurrence of any character.
- For example, the pattern “a? c” would match strings like “abc” and “axc.”
Unlike regular expressions, Wildcard patterns provide more intuitive and less complex means of matching strings.
Table of Contents
- What is Wildcard
What is Wildcard Pattern Matching
Wildcard Pattern Matching is a problem in identifying matching patterns that include wildcard characters. Consider a scenario where we are given a string and a pattern. Our goal is to check whether the entire string matches the given pattern. Our focus is on achieving a complete match, not a partial one. It is important to note that this algorithm specifically seeks complete matches, not partial ones.
Examples
Consider these examples to understand this pattern-matching problem.
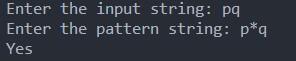
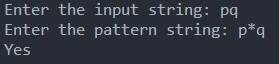
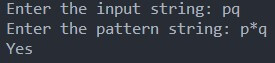
Example-1: Suppose the pattern is (p * q).
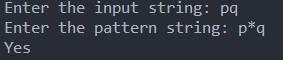
If the string is “pq,”
The pattern starts with ‘p’ and ends with ‘q’. Any character can be used between ‘p’ and ‘q’. Since the string begins with ‘p’ and ends with ‘q’ without containing any characters in between. So, this string “pq” completely matches the pattern (p * q).
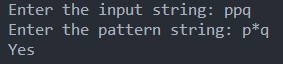
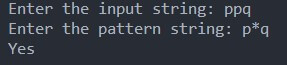
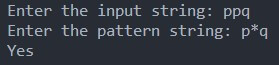
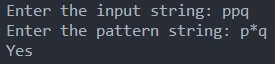
If the string is “ppq”
The string starts with ‘p,’ ends with ‘q,’ and contains the character ‘p’ between them. According to the pattern, characters between ‘p’ and ‘q’ are allowed. Therefore, this “ppq” string completely matches the (p * q) pattern.
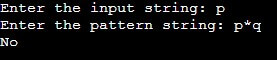
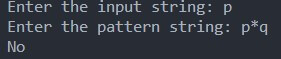
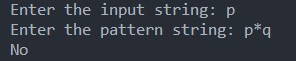
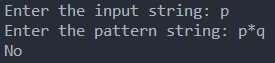
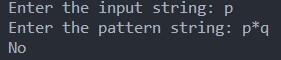
If the string is “p,”
Since the string does not end with the character ‘q.’ So, it does not match the given (p * q) pattern. So, the final result will be false.
If the string is “pqr,”
Since the string ends with the character ‘r’ instead of ‘q.’ It does not completely match the given (p * q) pattern. So, the final result will be false.
Example 2: Suppose the pattern is (p?q).
This pattern indicates that the string should begin with ‘p’ and end with ‘q.’ It should contain exactly one character between ‘p’ and ‘q’.
If the string is “ppq,”
since the string starts with ‘p,’ it ends with ‘q.’ It also contains precisely one character between ‘p’ and ‘q’. So, it completely matches the given pattern (p?q).
If the string is “pq,”
Although the string starts with ‘p’ and ends with ‘q’. But it contains no character between ‘p’ and ‘q’. So, this string does not match the given (p?q) pattern. Hence, the answer is false.
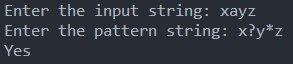
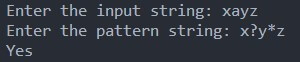
Example-3: Suppose the pattern is (x ? y * z)
This pattern indicates that any single character can exist between ‘x’ and ‘y’. It can contain 0 or more characters between ‘y’ and ‘z’.
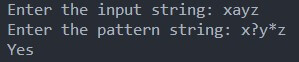
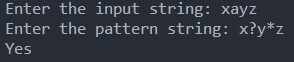
If the string is “xayz”
This string has just a single character between “x” and “y.”. It does not have a single character between ‘y’ and ‘z.’ Therefore, this “xayz” string satisfies the given (x ? y * z) pattern. Hence matches.
Suppose the string is “xyz”
Since no single character exists between ‘x’ and ‘y’ in this string. So, this string does not match the given (x ? y * z) pattern.
Consider another example with the pattern “file*.txt.” The algorithm will match file names starting with ‘file’ and ending with ‘.txt.’ Here, ‘*’ can denote any sequence of characters.
Note that you can verify these examples from any method code explained below.
Approaches to Solve the Wildcard Pattern Matching Problem
There are various ways to solve the Wildcard Pattern Matching Problem. These methods are different based on time and space. We will discuss important methods to solve this problem.
1. Brute-Force Approach
This is a naive approach to solving any problem. This is a straightforward method. In this method, you need to iterate through each possible substring in the given string. You must compare the substring with the wildcard pattern character by character in each step. Check for a match and continue until the entire string is processed.
Algorithm:
- First, we check if a string matches a pattern with ‘*’ and ‘?’.
- We use indexes to compare characters and handle ‘*’ as a wildcard.
- If there is no match. We backtrack to the last ‘*’ encountered.
- After checking if any pattern characters remain. We return false.
We will take inputs from the user in the code.
Implementation in C++
#include
using namespace std;
bool isMatch(string inputStr, string patternStr) {
int strIndex = 0, patternIndex = 0, lastWildcardIndex = -1, strBacktrackIndex = -1, nextToWildcardIndex = -1;
while (strIndex < inputStr.size()) {
if (patternIndex < patternStr.size() && (patternStr[patternIndex] == '?' || patternStr[patternIndex] == inputStr[strIndex])) {
++strIndex;
++patternIndex;
} else if (patternIndex < patternStr.size() && patternStr[patternIndex] == '*') {
lastWildcardIndex = patternIndex;
nextToWildcardIndex = ++patternIndex;
strBacktrackIndex = strIndex;
} else if (lastWildcardIndex == -1) {
return false;
} else {
patternIndex = nextToWildcardIndex;
strIndex = ++strBacktrackIndex;
}
}
for (int i = patternIndex; i < patternStr.size(); i++) {
if (patternStr[i] != '*') return false;
}
return true;
}
int main() {
string inputString, patternString;
cout << "Enter the input string: "; cin >> inputString;
cout << "Enter the pattern string: "; cin >> patternString;
if (isMatch(inputString, patternString))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}Output:
Case-1
Case-2
Case-3
Case-4
Time Complexity:
Best Case: O(min(N, M))
The best case occurs when there are no wildcard characters, and the loop runs until the shorter string is processed.
Worst Case: O(2^(N * M))
The worst case occurs when there are wildcard characters, and the algorithm needs to explore multiple possibilities.
In the average case, the time complexity of the brute force approach is O(2^(N * M)).
Space Complexity:
There is no extra space required except for constant variables. So the space complexity of this approach is O(1).
2. Recursive Backtracking
In backtracking, when an incorrect choice is encountered, the algorithm backtracks to backtrack to the previous state and processes for the next possible path to solve the problem. In this matching problem, recursive backtracking matches characters in the string in the given pattern. It backtracked when an incorrect choice occurred.
Algorithm:
- Base Case:
If both pointers (s_ptr and p_ptr) reach the end of their respective strings. Then return true.
- Wildcard Handling (‘*’):
If the current character in the pattern is ‘*’. Then try two possibilities:
- Match zero characters by moving the pattern pointer (p_ptr + 1).
- Match one character by moving the string pointer (s_ptr + 1).
- Character Matching (‘?’ and normal characters):
If the current characters match or the pattern has a ‘?’. Then, move both pointers to the next character.
- Backtracking:
If none of the conditions match. Then backtrack (return false).
- Recursion:
You can recursively call the function with updated pointers based on the chosen paths.
Implementation in C++
#include
using namespace std;
bool isMatch(string s, string p, int s_ptr, int p_ptr) {
// Base case: both pointers reach the end
if (s_ptr == s.length() && p_ptr == p.length())
return true;
// Handle wildcard character '*'
if (p_ptr < p.length() && p[p_ptr] == '*') {
// Try matching zero characters or one character
return isMatch(s, p, s_ptr, p_ptr + 1) || (s_ptr < s.length() && isMatch(s, p, s_ptr + 1, p_ptr));
}
// Match single character or '?'
if (s_ptr < s.length() && p_ptr < p.length() && (p[p_ptr] == '?' || p[p_ptr] == s[s_ptr]))
return isMatch(s, p, s_ptr + 1, p_ptr + 1);
// No match, backtrack
return false;
}
int main() {
string inputString, patternString;
cout << "Enter the input string: "; cin >> inputString;
cout << "Enter the pattern string: "; cin >> patternString;
if (isMatch(inputString, patternString, 0, 0))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}Output:
Case-1
Case-2
Case-3
Case-4
Time complexity:
Best Case: O(min(N, M))
The best case occurs when there are no wildcard characters, and the loop runs until the shorter string is processed.
Worst Case: O(2^(N * M))
The worst case occurs when there are wildcard characters, and the algorithm needs to check multiple possibilities.
Average Case: O(2^(N * M))
Space complexity:
O(N+M) is the depth of the recursive call.
3. Dynamic Programming (Memoization)
This approach uses a memoization table to store and retrieve already computed results to avoid redundant calculations. You can memoize results for subproblems to improve efficiency.
Algorithm:
- Create a table to remember solved problems.
- Begin with the last ‘text’ and ‘pattern’ characters.
- If both are empty, it is a match.
- If the ‘pattern’ is empty, no match.
- If ‘text’ is empty, check if ‘pattern’ has ‘*.’
- If ” found, try two ways: (a) ” is empty, (b) ‘*’ matches ‘text.’
- If other characters, check if it matches ‘text.’
- Move to the previous ‘text’ and ‘pattern’ characters.
Implementation in C++
#include
#include
using namespace std;
// Memoization table to store already computed results
vector<vector> memo;
// Function to check if a substring of 'text' matches the 'pattern'
int isPatternMatching(string& text, string& pattern, int textIndex, int patternIndex) {
// Base Cases
if (textIndex < 0 && patternIndex < 0)
return 1;
if (patternIndex < 0)
return 0;
if (textIndex < 0) { // If 'text' is empty, check if remaining characters in 'pattern' are all '*' while (patternIndex >= 0) {
if (pattern[patternIndex] != '*')
return 0;
patternIndex--;
}
return 1;
}
// If the result for this state has not been calculated
if (memo[textIndex][patternIndex] == -1) {
if (pattern[patternIndex] == '*') {
// Two options: '*' represents an empty string or it matches a character in 'text'
return memo[textIndex][patternIndex] =
isPatternMatching(text, pattern, textIndex - 1, patternIndex) ||
isPatternMatching(text, pattern, textIndex, patternIndex - 1);
} else {
if (pattern[patternIndex] != text[textIndex] && pattern[patternIndex] != '?')
return memo[textIndex][patternIndex] = 0;
else
return memo[textIndex][patternIndex] =
isPatternMatching(text, pattern, textIndex - 1, patternIndex - 1);
}
}
// Return the precomputed result
return memo[textIndex][patternIndex];
}
// Main function to check if 'text' matches 'pattern' using wildcard pattern matching
bool wildcardMatching(string text, string pattern) {
// Clear the memoization table and resize it
memo.clear();
memo.resize(text.size() + 1, vector(pattern.size() + 1, -1));
// Start the recursive matching process
return memo[text.size()][pattern.size()] =
isPatternMatching(text, pattern, text.size() - 1, pattern.size() - 1);
}
int main() {
string inputString, patternString;
cout << "Enter the input string: "; cin >> inputString;
cout << "Enter the pattern string: "; cin >> patternString;
if (wildcardMatching(inputString, patternString))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}Output:
Case-1
Case-2
Case-3
Case-4
Time complexity:
The quantity of resolved subproblems influences the time complexity. In this case, the total number of unique subproblems is O(M*N), i.e., the size of the DP table.
Therefore, the time complexity is O(M*N).
Space complexity:
Space complexity includes the memory used for memoization (DP table) of size O(M*N) and the depth of the recursion stack max(m, n). So, overall space complexity is O(M*N). Note that we can improve space complexity by using the results of the last row.
4. Dynamic Programming (Tabulation)
In this approach, we modify recursive Logic for Dynamic Programming. In the recursive logic, we used the base case to check (i < 0) and (j < 0). But, since we cannot set the dp array index to -1. So, we shift every index by 1 towards the right.
Algorithm
These are the steps used:
- Initialize a dp array of size [n+1][m+1] with zero values.
- Set the base conditions (keeping in mind 1-based indexing):
- Set the top-left cell as ‘True’.
- Set the values of the first column as ‘False.’
- For the first row, apply the isAllStars() function for every cell value.
- Implement the recursive code while considering the shifted indexes (S1[i] becomes S1[i-1] and similarly for S2).
- Finally, print dp[n][m] as the answer.
Implementation in C++
#include
#include
using namespace std;
// Function to check if a substring of str contains only '*'
bool containsOnlyStars(string &str, int index) {
// str is taken in 1-based indexing
for (int i = 1; i <= index; i++) {
if (str[i - 1] != '*')
return false;
}
return true;
}
// Function to perform wildcard pattern matching between pattern and text
bool wildcardPatternMatching(string &pattern, string &text) {
int patternLength = pattern.size();
int textLength = text.size();
// Create a DP table to memoize results
vector<vector> dp(patternLength + 1, vector(textLength + 1, false));
// Initialize the first row and column
dp[0][0] = true;
for (int j = 1; j <= textLength; j++) {
dp[0][j] = false;
}
for (int i = 1; i <= patternLength; i++) {
dp[i][0] = containsOnlyStars(pattern, i);
}
// Fill in the DP table
for (int i = 1; i <= patternLength; i++) {
for (int j = 1; j <= textLength; j++) {
if (pattern[i - 1] == text[j - 1] || pattern[i - 1] == '?') {
dp[i][j] = dp[i - 1][j - 1];
} else {
if (pattern[i - 1] == '*') {
dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
} else {
dp[i][j] = false;
}
}
}
}
// The value at dp[patternLength][textLength] contains whether pattern matches text
return dp[patternLength][textLength];
}
int main() {
string inputString, patternString;
cout << "Enter the input string: "; cin >> inputString;
cout << "Enter the pattern string: "; cin >> patternString;
if (wildcardPatternMatching(patternString, inputString))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}Output:
Case-1
Case-2
Case-3
Case-4
Time complexity:
O(M*N) size of DP table.
There are nested loops iterated over the lengths of the pattern and text strings. This is the size of the product of their lengths. The dynamic programming table (dp array) of size (N + 1) x (M + 1) is filled using these nested loops.
Space complexity:
O(M*N) size of DP table.
Note that we can improve space complexity by using the results of the last row. This improved space complexity approach is explained below.
5. DP tabulation with Space Optimization
In the given relation of the above dynamic programming tabulation approach:
dp[i][j] = dp[i − 1][j − 1],
dp[i][j] = dp[i − 1][j] ∣∣ dp[i][j − 1]
You can see that to compute a value in the dp array. We only need the previous row values (denoted as prev) and the current row previous column values. We do not need to store the entire array to optimize space here.
Algorithm:
These are the steps for space optimization:
- We use two rows: prev and cur.
- Initialize both rows based on the base condition. For the previous row, set its first value to True and the rest to False. When declaring the cur variable, initialize its first cell value using the isAllStars() function.
- Implement the memoization logic. You can replace dp[i-1] with prev and dp[i] with cur.
- After each inner loop execution, set prev equal to cur for the next iteration.
- Finally, return prev[m] as the answer.
Implementation in C++
#include
#include
using namespace std;
// Function to check if a substring of text contains only '*'
bool containsOnlyAsterisks(string &text, int index) {
// text is taken in 1-based indexing
for (int i = 1; i <= index; i++) {
if (text[i - 1] != '*')
return false;
}
return true;
}
// Function to perform wildcard pattern matching between pattern and inputString
bool wildcardPatternMatching(string &pattern, string &inputString) {
int patternLength = pattern.size();
int inputStringLength = inputString.size();
// Create two arrays to store previous and current rows of matching results
vector previousRow(inputStringLength + 1, false);
vector currentRow(inputStringLength + 1, false);
previousRow[0] = true; // Initialize the first element of the previous row to true
for (int i = 1; i <= patternLength; i++) {
currentRow[0] = containsOnlyAsterisks(pattern, i); // Initialize the first element of the current row
for (int j = 1; j <= inputStringLength; j++) {
if (pattern[i - 1] == inputString[j - 1] || pattern[i - 1] == '?') {
currentRow[j] = previousRow[j - 1]; // Characters match or pattern has '?'
} else {
if (pattern[i - 1] == '*') {
currentRow[j] = previousRow[j] || currentRow[j - 1]; // '*' represents empty or a character
} else {
currentRow[j] = false; // Characters don't match and pattern[i-1] is not '*'
}
}
}
previousRow = currentRow; // Update the previous row with the current row
}
// The value at previousRow[inputStringLength] contains whether pattern matches inputString
return previousRow[inputStringLength];
}
int main() {
string inputString, patternString;
cout << "Enter the input string: "; cin >> inputString;
cout << "Enter the pattern string: "; cin >> patternString;
if (wildcardPatternMatching(patternString, inputString))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}Output:
Case-1
Case-2
Case-3
Case-4
Time complexity:
O(N*M)
There are nested loops iterated over the lengths of the pattern and text strings. This is the size of the product of their lengths, i.e., O(N*M).
Space complexity:
O(M) space. This approach uses two vectors (previousRow and currentRow) of size M + 1.
6. Greedy Approach
The Greedy method finds temporary best solutions and hopes for global optimality. You can solve wildcard pattern-matching problems using greedy techniques. The algorithm is given in steps below.
Algorithm:
- Initialize pointers i, j at text and pattern beginnings.
- Set startIndex and match it to -1 and 0, respectively.
- Loop through text until the end or non-matching character.
- If characters match, move to next in both pattern and text.
- If the pattern has ‘?’, move to next in both pattern and text.
- If the pattern has ‘*’, mark current positions as a proper match.
- If no match and no ”, backtrack to the last ” position.
- Loop over text and consume any remaining ‘*’ in the pattern.
- If the end of both pattern and text is reached, the pattern matches the text.
Implementation in C++
#include
using namespace std;
bool customPatternMatching(string input, string wildcardPattern) {
int inputLength = input.length();
int patternLength = wildcardPattern.length();
int i = 0, j = 0, startIndex = -1, match = 0;
while (i < inputLength) {
if (j < patternLength && (wildcardPattern[j] == '?' || wildcardPattern[j] == input[i])) {
i++;
j++;
} else if (j < patternLength && wildcardPattern[j] == '*') {
startIndex = j;
match = i;
j++;
} else if (startIndex != -1) {
j = startIndex + 1;
match++;
i = match;
} else {
return false;
}
}
while (j < patternLength && wildcardPattern[j] == '*') {
j++;
}
return j == patternLength;
}
int main() {
string inputString, patternString;
cout << "Enter the input string: "; cin >> inputString;
cout << "Enter the pattern string: "; cin >> patternString;
if (customPatternMatching(inputString, patternString)) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
}
return 0;
}Output:
Case-1
Case-2
Case-3
Case-4
Time complexity:
O(N*M)
You need to iterate over the characters of both strings.
Space complexity:
O(1)
This greedy approach does not use any extra space except constant variable spaces.
Best Approaches
The optimal approach varies depending on the specific needs of the problem at hand. Brute force is simple but inefficient (exponential time complexity) for large inputs. Dynamic Programming provides efficiency but has higher space complexity. When choosing a method, you should consider factors such as time and space efficiency, simplicity, and the nature of the input data. Generally, people use Dynamic programming solutions.
Summary and Comparisons of Discussed Approaches
The Summary of these 6 methods is given in the following table.
| Approach | Time Complexity | Space Complexity | Pros | Cons |
| Brute-Force | O(2^(N * M)) | O(1) | Simple, easy to implement. | Inefficient for large inputs, exponential time complexity. |
| Recursive Backtracking | O(2^(N * M)) | O(N + M) | Concise, easy to understand. | Exponential time complexity, maybe slow for large inputs. |
| Dynamic Programming (Memoization) | O(M * N) | O(M * N) | Efficient, avoids redundant calculations. | Higher space complexity, recursion stack depth. |
| Dynamic Programming (Tabulation) | O(M * N) | O(M * N) | Efficient, avoids redundant calculations. | Higher space complexity. |
| DP Tabulation with Space Optimization | O(N * M) | O(M) | Efficient, reduced space usage. | It still uses additional space for DP rows. |
| Greedy Approach | O(N * M) | O(1) | Simple, low space usage. | May not be optimal for all cases, limited flexibility. |
Comparison between wildcards and regular expressions
Since this Wildcard Pattern Matching problem is related to wildcards (? and *). So, let’s compare wildcards and regular expressions for better understanding.
| Section | Wildcards | Regular Expressions |
| Syntax | Limited syntax with ‘*’ and ‘?’ | Extensive syntax with various symbols, metacharacters, and operators for complex patterns. |
| Complexity | Simpler, suitable for basic matching | It is more complex and supports advanced features like grouping, quantifiers, and character classes. |
| Characters | Typically ‘*’ and ‘?’ | Wide range of metacharacters and operators for precise character matching. |
| Matching Scope | Primarily used for simple matching tasks like file names. | Suitable for complex pattern matching, text processing, data validation, and extraction. |
| Learning Curve | Easier to grasp and use for basic tasks. | Steeper learning curve due to the variety of features and syntax. |
| Performance | Generally faster for simple patterns. | May have higher processing overhead for complex patterns. |
| Use Cases | Ideal for scenarios where simplicity suffices, such as basic string or file name matching. | Suited for advanced applications requiring intricate pattern recognition and manipulation. |
| Common Symbols | ‘*’ (any sequence) and ‘?’ (single character). | ‘.’, ‘*,’ ‘+,’ ‘?’, ‘^,’ ‘$,’ etc., offering a broader range of matching capabilities. |
| Examples | – Pattern: file*.txt
– Pattern: a?c |
– Pattern: ^\d{3}-\d{2}-\d{4}$ (Social Security Number)
– Pattern: ^([a-zA-Z0-9_.+-])+@[a-zA-Z0-9-]+\.[a-zA-Z0-9-.]+$ (Email address) |
Conclusion
Wildcard has two special symbols: * (Asterisk), which has zero or more characters, and ? (Question Mark), which has a single character.
Wildcard Pattern Matching is a problem that identifies patterns that contain wildcard characters (‘*’ and ‘?’) within a given string. In this problem, you need to check whether the entire string matches the given pattern. You need to achieve a complete match but not a partial match. There are various ways to solve this problem like Brute-Force, Dynamic programming, and Greedy technique. Each approach has its advantages and drawbacks regarding time and space complexity, simplicity, and efficiency.
FAQs (Frequently Asked Questions)
Q1. How do wildcards differ from regular expressions?
Answer: Wildcards have a limited syntax and primarily use ‘*’ and ‘?’. Wildcards are suitable for simple matching tasks like file names. Whereas Regular expressions have more syntax with various metacharacters and operators. You can build more pattern recognition and manipulation using Regular expressions.
Q2. How do you handle case-insensitive matching in Wildcard Pattern Matching?
Answer: If you want to perform case-insensitive matching, you need to include the header “#include <cctype>.” Then you can use functions like tolower() and toupper() to convert characters to lowercase and uppercase before comparing them.
Q3. Can Wildcard Patterns be used in database queries?
Answer: Yes. Wildcard patterns (with the use of ‘*’ and ‘?’) are mostly used in database queries to perform pattern-based searches. You can match and retrieve records based on partial or variable information.
Q4. How can Wildcard Patterns be used in file search operations?
Answer: Wildcard patterns can be used in file search operations to match and filter filenames based on specific patterns. For example, a pattern like *.txt could be used to find all files with a “.txt” extension in a directory.
Q5. Can Wildcard Patterns handle matching for non-alphanumeric characters?
Answer: Yes. Wildcard patterns can be used to match non-alphanumeric characters like symbols and punctuation. For example, a pattern like `*data*` could match strings containing the word “data” surrounded by any characters.
Recommended Articles
We hope this EDUCBA information on “Wildcard Pattern Matching” benefited you. You can view EDUCBA’s recommended articles for more information.