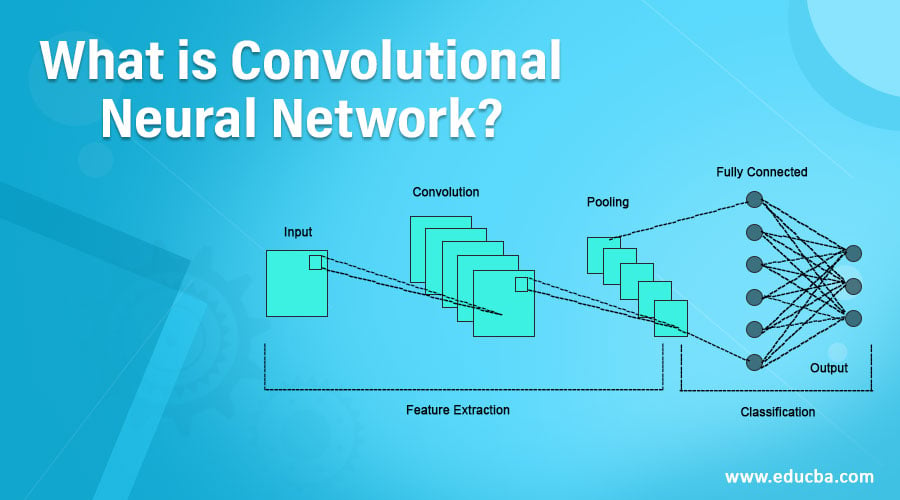
Introduction to Convolutional Neural Network
Many image analysis tasks, such as image classification and medical picture analysis, are carried out using convolutional neural networks (CNNs). They are made specifically to process inputs and extract useful information that can be used to distinguish between various output categories.
A convolutional neural network consists of an associate degree input, associate degrees, an output layer, and multiple hidden layers. The hidden layers of a CNN usually contain a series of convolutional layers that twist with multiplication or actual alternative number.
A convolutional layer inside a neural network ought to have the subsequent attributes:
- Convolutional kernels outlined by a dimension and height
- The variety of input channel and output channels
- The depth of the convolutional filter should be capable of the amount channels of the input feature map.
Features of Convolutional Neural Network
Convolutional neural networks have the following characteristic features:
- The convolutional neural network layers have neurons organized in three. They’re weight, height, and depth.
- Local property: They exploit the spatial section by implementing a neighborhood connectivity pattern between neurons of adjacent layers.
- Shared weights: Every filter is replicated across the complete visual view.
- Pooling: A convolutional neural network divides feature maps into rectangular sub-regions during pooling layers. The characteristics are averaged or maximized within each sub-region before being down-sampled to a single value.
Additional Hyperparameters
Convolutional neural networks use additional hyperparameters than a standard multilayer perceptron. We use specific rules while optimizing. They are:
- A number of filters: During this feature, map size decreases with depth; thus, layers close to the input layer can tend to possess fewer filters, whereas higher layers will have additional ones. Protective additional data concerning the input would need to keep the overall variety of activations non-decreasing from one layer to ensuring.
- Filter shape: During this, the filter form is predicated on the dataset. We want to find the proper level to find the filter form with none.
- Max pooling shape: During this, selecting the larger shapes ends up in cut back the dimension of the signal, and it would lead to excess data
Different Layers
Different layers make up a convolutional neural network, which transforms the input layer into the associate degree output layer.
- Convolutional Layer
- Pooling Layer
- Rectified Long Measurelayer
- Fully Connected Layer
- Loss Layer
Parameters
The convolutional layer consists of various parameters,
- Local Property
- Spatial Arrangement
- Parameter Sharing
Regularization
Convolutional neural networks use varied forms of regularization. They are:
- Empirical Regularization
- Explicit Regularization
Empirical
Under empirical regularization, we tend to have the following:
- Dropout: Dropout is one every of the foremost effective regularization techniques to possess that emerged within a previous couple of years. The fundamental plan behind the dropout is to run every iteration of the scenery formula on haphazardly changed versions of the first DLN.
- Drop connect: It is the generalization of dropout. Drop Connect is comparable to dropout because it introduces active meagerness inside the model. This drop connect works the same as that of dropout, but the difference is that we use nodes instead of weights.
- Stochastic pooling: Rather than following fixed pooling rules, random pooling selects activations within each pooling region based on a multinomial distribution determined by the activities within that region. In random pooling, we tend to choose the pooled map response by sampling from a multinomial distribution fashioned from the activations of every pooling region.
- Artificial data: To mitigate overfitting in convolutional networks, providing additional training examples can be beneficial.
Explicit
Under express regularization, we tend to have the following:
- Early Stopping: It involves evaluating the loss function on the training dataset at the end of each training epoch.
- Number of Parameters: In CNN, the filter size additionally affects the number of parameters. Restricting the number of parameters limits the prognosticative power of the network directly; a reduction in the quality will operate that it will discharge on the information, and therefore limits the number of overfitting.
- Weight Decay: Weight decay is the simpler king of regularization that merely adds a further error, proportional to the total of weights or square magnitude of the load vector, to the error at every node.
- Max Norm Constraints: Regularization is to enforce associate degree absolute boundary on the magnitude of the load vector for each vegetative cell and use projected gradient descent to enforce the constraint.
Applications of Convolutional Neural Network
Convolutional neural networks are employed in many applications. A number of them are mentioned below:
- It is employed for video analysis
- Used for language process
- Drug discovery
- Health risk assessment
- Checkers game
- Time series prognostication
Conclusion
In this, we learn about the convolutional neural networks
- Its features
- Rules for optimization
- Layers of CNN
- Regularizations used for CNN
- Applications
Recommended Articles
We hope that this EDUCBA information on “What is Convolutional Neural Network?” was beneficial to you. You can view EDUCBA’s recommended articles for more information.