Updated July 26, 2023

Definition of Standard Deviation Examples
The following article provides an outline for Standard Deviation Examples. There are ample examples of standard deviations. Standard deviation is the measure of the dispersion of the dataset i.e., how spread out the numbers are. It is useful for comparing different data sets that might have the same mean but a different range.
The following different Standard deviation example gives an understanding of the most common situations where the Standard deviation is calculated and how one can calculate the same.
Examples of Standard Deviation
Below are examples of the Standard Deviation:
Standard Deviation – Example #1
The stock of Company Z sells for $ 50 per share, and the same offer the following payoffs for the next year:
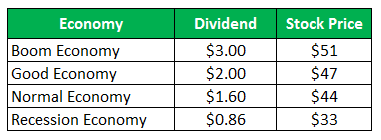
Calculate the Standard deviation when all four scenarios are given are equally likely.
Solution:
Calculations of Holding Period Return (HPR) are as follows –
Formula of HPR
For Boom Economy
- HPR (Boom) = ((51-50) + 3)/50 = 8.00%
- HPR (Good) = ((47-50) + 2)/50 = -2.00%
- HPR (Normal) = ((44-50) + 1.60)/50 = -8.80%
- HPR (Recession) = ((33-50) + 0.86)/50 = -32.28%
Calculation of Expected Return
Since all the scenarios are equally likely, the probability of all will be ¼
The formula of Expected Return
- Expected Return = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8.80 %) + (1/4 x -32.28 %)
- Expected Return = -8.77 %
Calculation of Standard Deviation
Formula of Variance
- Variance = 1/4 (8 – (-8.77)) 2 + 1/4 (-2 – (-8.77)) 2 + 1/4 (-8.80 – (-8.77)) 2 + 1/4 (-32.28 – (-8.77)) 2
- Variance = 219.95
The formula of Standard Deviation
The standard Deviation will be the Square Root of Variance.
Standard Deviation = √Variance
- Standard Deviation= √219.95
- Standard Deviation = 14.83%
Standard Deviation Example – 2
Standard deviation in the case of two companies in the portfolio
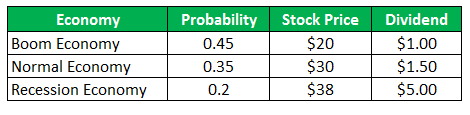
The common stock of Company A sells for $ 28 per share, and the same offers following payoffs for the next year
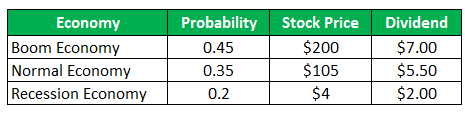
The common stock of Company B sells for $ 93 per share, and the same offers the following payoffs for the next year:
(a) Calculate the standard deviation of Company A
(b) Calculate the standard deviation of Company B
(c) Calculate the standard deviation of the portfolio if half of the investment is made in Company A and the rest half in Company B
Solution:
For Company A
Calculations of Holding Period Return (HPR)
Formula of HPR
HPR = ((End of Period Value – Original Value) + Income) / Original Value) * 100
- HPR (boom) = ((20-28) + 1)/28 = -25.00%
- HPR (Normal) = ((30-28) + 1.50/28 = 12.50%
- HPR (Recession) = ((38-28) + 5)/28 = 53.57%
Calculation of Expected Return of Company A
Formula of Expected Return
Expected Return = (Probability of Boom * Return from Boom) + (Probability of Normal * Return from Normal) + (Probability of Recession * Return from Recession)
- Expected Return= (0.45 x -25.00%) + (0.35 x 12.50%) + (0.20 x 53.57%)
- Expected Return = 3.84%
Calculation of Standard Deviation Company A
Formula of Variance
Variance=[Probability of Boom * (Return from Boom – Total Expected Return) 2] + [Probability of Normal * (Return from Normal – Total Expected Return) 2] + [Probability of Recession * (Return from Recession – Total Expected Return) 2]
- Variance= 0.45(-25.00 – (3.84)) 2 + 0.35 (12.50 – (3.84)) 2 + 0.20 (53.57 – (3.84)) 2
- Variance= 895.15
The formula of Standard Deviation
The standard Deviation will be the Square Root of Variance.
Standard Deviation = √Variance
- Standard Deviation = √895.15
- Standard Deviation = 29.92%
For Company B
Calculations of Holding Period Return (HPR)
Formula of HPR
HPR = ((End of Period Value – Original Value) + Income) / Original Value) * 100
HPR (Boom) = ((200-93)+7)/93 = 122.58%
HPR (Normal) = ((105-93)+5.50/93 = 18.82%
HPR (Recession) = ((4-93)+2)/93 = -93.55%
Calculation of Expected Return
Formula of Expected Return
- Expected Return= (0.45x 122.58%) + (0.35 x 18.82%) + (0.20 x -93.55%)
- Expected Return = 43.04%
Calculation of Standard Deviation
Formula of Variance
Variance=[Probability of Boom * (Return from Boom – Total Expected Return) 2] + [Probability of Normal * (Return from Normal – Total Expected Return) 2] + [Probability of Recession * (Return from Recession – Total Expected Return) 2]
- Variance= 0.45 (122.58– (43.04)) 2+ 0.35 (18.82– (43.04)) 2+ 0.20 (-93.55– (43.04)) 2
- Variance= 6783.65
The formula of Standard Deviation
The standard Deviation will be the Square Root of Variance.
Standard Deviation = √Variance
- Standard Deviation =√6783.65
- Standard Deviation = 82.36 %
Calculation of the Expected Return and Standard Deviation of a Portfolio half Invested in Company A and half in Company B.
Standard Deviation of Company A=29.92%
Standard Deviation of Company B=82.36%
Weight of Company A = 0.50
Weight of Company B = 0.50
The formula of Standard Deviation of Portfolio
- Standard Deviation of Portfolio = (0.50 * 29.92) + (0.50 * 82.36)
- Standard Deviation of Portfolio= 56.14%
Analysis
The portfolio standard deviation is lower than for either stock’s individual because the stocks are diversified in different stocks. Diversification leads to a reduction in risk unless a perfect correlation exists between returns on portfolio investments.
Conclusion
The standard deviation measures the dispersion of the dataset, which is relative to its mean. It is calculated as the square root of variance. The greater is the standard deviation of the security; the greater will be the variance between each price and the mean, which shows that the price range is large. The above-mentioned examples are some examples of Standard deviation in different ways. There are various other examples that show that Standard deviation can be calculated using other data.
Recommended Articles
This has been a guide to the standard Deviation Examples. Here we discuss the various examples of standard deviation along with a detailed explanation. You may also have a look at the following articles to learn more –


