Updated July 5, 2023

Definition of Skip List Data Structure
The Skip List is a probabilistic data structure that extends the linked list concept. Linear data structures known as linked lists hold individual objects, with nodes comprising the data and a reference to the next node. We build subsequent layers of linked lists here by using probability concepts on top of an original linked list. The additional layer of links has fewer elements with no new elements. Using a skip list, users may be able to find, remove, and insert elements into the queue. Lastly, as the name suggests, it skips non-required elements to perform its task as required.
Syntax
A skip list allows a data structure that enables fast search capabilities. The lowest layer of a Skip List data structure contains elements and connects with a list of lists that maintains a linked hierarchy of subsequences, where it skips over certain elements. We mentioned 3 skip list operations: Insert, Search, and Delete. Here we will look at the pseudo-code so that when we deep dive into understanding the working of the skip list, the mapping back of working to pseudocode will absorb the scene of the larger picture.
Pseudo for inserting:
Input-> key/value which needs to be inserted
index_key = Search(key) //Use of search function
q = null
counter_index = 1
repeat
counter_index = counter_index + 1 //Noting tower height of element
if counter_index >= h
h = h + 1
createNewLevel()//New level in linked list created
while (index_key.above == null)
index_key = index_key.prev
index_key = index_key.above
q = insertAfter(key, index_key) //Insert key after position index_key
until random() == '0'
n = n + 1
return qPseudocode for searching:
Input -> key/value which needs to be searched
pointer = start //Initialize the pointer to start
repeat till there is a level lower:
pointer = below(pointer)
repeat till key/value >= value(pointer of the next value):
pointer = next(pointer)Pseudocode for deletion:
Input -> key
All positions are searched for availability of the key
if there is no match
return empty
else
repeat base level to the header level
if the element is present in the layer, bypass the node and connect the previous node to the next node and vice versa How Does Skip List Work in Data Structure?
To understand the working of a skip list, we need to understand the working of 3 operations allowed in a skip list. To start off, we take the key that needs to be searched as input in the search operation. We check the current node’s value because the list is sorted. Now the idea here is to keep searching on the same level till the key of the next node doesn’t become larger than the search key. As soon as it becomes greater, we move on level down and repeat the same thing until we reach the base level, after which we can’t go down.
Now, in the insert, we use the idea of the search to search for any given key before we insert the value. Keep searching if the key of the next node is smaller than the key to be inserted, and if yes, continue searching. If the next node’s value is higher, we move a level down until we reach the base level. Now at the base level, we keep searching until the next node’s value is smaller and traversing, and as soon as it becomes larger, we know we would have to insert the value here and do the same. We use a random function to generate the condition that if the number we inserted moves as a potential value in subsequent higher levels and places itself as one of the search keys in those higher levels.
Finally, we search for the key we want to delete in case of deletion. Now, we try to bypass the node that would get deleted and connect the node on its left to the node on its right, making a list feel that the value doesn’t exist in the list as it has now been bypassed, and the connection is broken. If the value is present, we start moving up and perform the same operation. The moment we see that the value is not present in the higher layer is when we stop.
Now that we know the working of all the 3 operations, we must look at a hands-on example to understand the piece much better!
Example
Implementation of circular Queue:
Syntax:
import random
class Node(object):
def __init__(self, key, level):
self.key = key
self.forward = [None]*(level+1)
class SkipList(object):
def __init__(self, max_lvl, P):
self.LEVEL_MAX = max_lvl
self.P = P
self.header = self.newNodeCreate(self.LEVEL_MAX, -1)
self.level = 0
def newNodeCreate(self, lvl, key):
n = Node(key, lvl)
return n
def randomLvlGenerate(self):
lvl = 0
while random.random() self.level:
for i in range(self.level+1, rlevel+1):
update[i] = self.header
self.level = rlevel
n = self.newNodeCreate(rlevel, key)
for i in range(rlevel+1):
n.forward[i] = update[i].forward[i]
update[i].forward[i] = n
print("Insertion successful for {}".format(key))
def deleteFunc(self, search_key):
update = [None]*(self.LEVEL_MAX+1)
current = self.header
for i in range(self.level, -1, -1):
while(current.forward[i] and \
current.forward[i].key < search_key): current = current.forward[i] update[i] = current current = current.forward[0] if current != None and current.key == search_key: for i in range(self.level+1): if update[i].forward[i] != current: break update[i].forward[i] = current.forward[i] while(self.level>0 and\
self.header.forward[self.level] == None):
self.level -= 1
print("Deletion successful for {}".format(search_key))
def searchFunc(self, key):
current = self.header
for i in range(self.level, -1, -1):
while(current.forward[i] and current.forward[i].key < key):
current = current.forward[i]
current = current.forward[0]
if current and current.key == key:
print("The search key {} is found in the list".format(key))
def printSkipList(self):
print("\n*****The Skip List is as follows:******")
head = self.header
for lvl in range(self.level+1):
print("@ Level {}: ".format(lvl), end=" ")
node = head.forward[lvl]
while(node != None):
print(node.key, end=" ")
node = node.forward[lvl]
print("")
def main():
lst = SkipList(3, 0.5)
print("----Insert mode----")
lst.InsertFunc(27)
lst.InsertFunc(9)
lst.InsertFunc(91)
lst.InsertFunc(92)
lst.InsertFunc(11)
lst.InsertFunc(72)
lst.InsertFunc(36)
lst.InsertFunc(45)
lst.InsertFunc(54)
lst.InsertFunc(18)
lst.InsertFunc(81)
lst.InsertFunc(99)
lst.printSkipList()
print("----Search mode----")
lst.searchFunc(72)
print("----Delete mode----")
lst.deleteFunc(92)
lst.printSkipList()
main()Output:
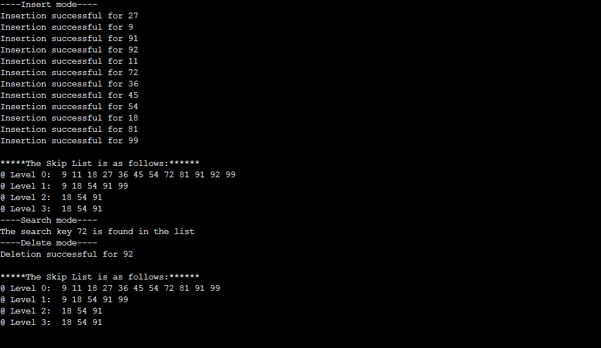
Conclusion
In this article, we looked at the 3 operations that skip list offers and a hands-on example that completes the learning of skip list data structure with a practical touch! Try to run the code multiple times in the code, and you will see the elements in the levels changing with each run!
Recommended Articles
We hope that this EDUCBA information on “Skip List Data Structure” was beneficial to you. You can view EDUCBA’s recommended articles for more information.

