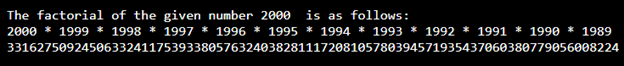Updated October 10, 2023
What is a Recursive Function?
The recursive Function in Python is used for repetitively calling the same function until the loop reaches the desired value during the program execution using the divide-and-conquer logic. One of the obvious disadvantages of using a recursive function in the Python program is that if the recurrence is not a controlled flow, it might consume a solid portion of system memory. To rectify this problem, an incremental conditional loop can replace the Recursive function in a Python programming language.
Table of Contents
- What is a Recursive Function?
- Python Code – Recursion vs Iteration
- Examples of Python Recursion
- Advantages and Disadvantages
The concept of recursion remains the same in Python. The function calls itself to break down the problem into smaller problems. The simplest example of recursion would be finding the factorial of a number.
Let’s say we need to find the factorial of 5 => 5! (Our problem)
To find 5! The problem can be broken into smaller ones: 5! => 5 x 4!
So, to get 5! We need to find 4! and multiply it with 5.
Let’s keep on dividing the problem
5! = 4! x 5
4! = 3! x 4
3! = 3 x 2!
2! = 2 x 1!
1! = 1
When it reaches the smallest chunk, i.e., getting the factorial of 1, we can return the result as 120.
Algorithm for factorial
Let us see the algorithm for factorial:
function get_factorial(n):
if n < 2:
return 1
else:
return get_factorial(n-1)Function calls
Suppose we are finding a factorial of 5.
get_factorial(5) 5 * get_factorial(4) = returns 120 #1st call
get_factorial(4) 4 * get_factorial(3) = returns 24 #2nd call
get_factorial(3) 3 * get_factorial(2) = returns 6 #3rd call
get_factorial(2) 2 * get_factorial(1) = returns 2 #4th call
get_factorial(1) returns 1 #5th callThe result will be 120, where we started the execution of the function. Our recursion function will stop when the number is so reduced that the result can be obtained.
- The first call, which is getting the factorial of 5, will result in a recursive condition where it will be added to the stack, and another call will be made after reducing the number to 4.
- This recursion will keep calling and breaking the problem into smaller chunks until it reaches the base condition.
- The base condition here is when the number is 1.
- Every recursive function has its recursive condition and a base condition.
Python Code – Recursion vs Iteration
We understood what recursion is and how it works in Python, as we know all languages have different implementations of recursion for memory and computational optimizations. There can be a case where iteration would be faster than recursion.
Here, we would compare recursion and iteration methods to see how Python performs in both cases.
# Recursive function to calculate factorial
def get_recursive_factorial(n):
if n < 0:
return -1
elif n < 2: # Base condition
return 1
else:
return n * get_recursive_factorial(n - 1) # Recursion condition
# Iterative function to calculate factorial
def get_iterative_factorial(n):
if n < 0:
return -1
else:
fact = 1
for i in range(1, n + 1):
fact *= i
return fact
# Printing Results
print(get_recursive_factorial(6)) # Output: 720
print(get_iterative_factorial(6)) # Output: 720Output:
As we can see, both give the same output as we have written the same logic. Here, we can’t see any difference in execution.
Let’s add some time code to get more information about the execution of recursion and iteration in Python.
We will import the “time” library and check what time recursion and iteration take to return the result.
Code with time calculation
import time
def get_recursive_factorial(n):
if n < 0:
return -1
elif n < 2:
return 1
else:
return n * get_recursive_factorial(n - 1)
def get_iterative_factorial(n):
if n < 0:
return -1
else:
fact = 1
for i in range(1, n + 1):
fact *= i
return fact
start_time = time.time()
get_recursive_factorial(100)
print("Recursion--- %s seconds ---" % (time.time() - start_time))
start_time = time.time()
get_iterative_factorial(100)
print("Iteration--- %s seconds ---" % (time.time() - start_time))We will do repeated executions with a different value for factorial and see the results. The below results could vary from machine to machine.
Case 1:- Factorial of 6
Case 2: Factorial of 50
Case 3: Factorial of 100
Case 4: Factorial of 500
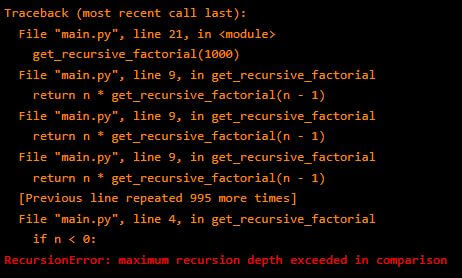
Case 5: Factorial of 1000
We have analyzed both methods in a different problem. Moreover, both have performed similarly except for case 4.
In case 5, we got an error while doing it with recursion.
Python has a restriction on the maximum depth you can go with recursion, but the same problem could be solved with iteration.
Python has restrictions against the problem of overflow. Python is not optimized for tail recursion, and uncontrolled recursion causes a stack overflow.
The “sys.getrecursionlimit()” function would tell you the limit for recursion.
The recursion limit can be changed but is not recommended; it could be dangerous.
Examples of Python Recursion
Now let us demonstrate how the recursive function works in python with examples as follows:
Example #1
Code:
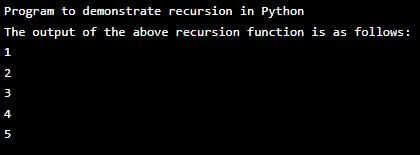
print("Program to demonstrate recursion in Python")
def rcur_func(x):
if(x>=1):
rcur_func(x-1)
print(x)
print("The output of the above recursion function is as follows:")
rcur_func(5)Output:
In the above program, we can see we have defined a function “rcur_func()” to this function, we are passing an integer variable “x”, and then we are checking for the condition using an “if” statement such as if (x >= 1 ) and if the condition is satisfied, then it enters the if loop and where it calls the same function again and passes the argument by decrementing the x value by 1 ( x-1 ). Therefore, we have passed the x value as “5” to the defined function in the above program. When 5 is given to the “if” statement, the condition is satisfied; hence, the if loop results in “true” and enters the loop. Again, the same function is called by passing the decremented by 1 x value ( x =5 -1 ); now the x value is four again, it will be checked by the “if” statement, and the “if” loop condition is satisfied and results “true” and enters the loop, and again the function is called by passing the decremented by 1 x value ( x= 4 – 1). This process is continued until the if statement condition results false until the x value reaches 1. Then, the output will print the values of the above recursion as 1, 2, 3, 4, and 5, as shown in the above screenshot. It will print only till five as the integer value passed to the recursion function is 5, and if we pass integer value 9, then it will print till 9.
Now, let us see the termination condition in the recursion concept. In Python, as discussed above, it is very important for a recursive function to have a termination condition because if the condition is not specified, it may lead to infinite loop recursion, which never terminates the program. Therefore, the recursion function needs to have a termination condition. Now, let us take a famous example of finding the factorial of the given number.
So, to find the factorial of a given number “z”, we calculate it as z = z * (z -1) until z is greater than 1; we need to compute this expression, and if z = 0, then the above factorial expression will result in 1. So, let us demonstrate programmatically in the below example.
Example #2
Code:
print("Program to demonstrate recursion termination condition in factorial of number")
def factorial_func(z):
if z == 1:
print(z)
return 1
else:
print (z,'*', end=' ')
return (z * factorial_func(z-1))
z = 5
print("The factorial of the given number", z," is as follows:")
print(factorial_func(z))Output:
In the above program, we can see how we have calculated the factorial of the given number 5, and the result is as displayed in the above screenshot.
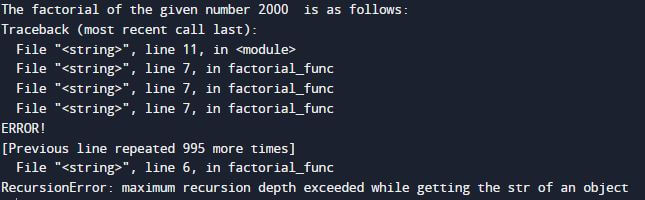
In Python, there is a recursion limit; unlike in other programming languages, we can create an infinite loop. So, to check the recursion limit in the Python program, we have to use the sys module. In Python, if we are trying to calculate the above factorial function by passing the value of z as 3000, then it will give us a runtime error or RecursionError saying “maximum recursion depth is exceeded” because in Python, by default, the recursion function call stops after 1000. To change this limit, we must use the sys module’s “setrecursionlimit()” to the desired value. Now, let us demonstrate this in the below example.
Example #3
Code:
def factorial_func(z):
if z == 1:
print(z)
return 1
else:
print (z,'*', end=' ')
return (z * factorial_func(z-1))
z = 2000
print("The factorial of the given number", z," is as follows:")
print(factorial_func(z))Output:
So we can avoid the above problem by using the sys module with setrecursionlimit() in the below program.
Code:
import sys
sys.setrecursionlimit(3000)
def factorial_func(z):
if z == 1:
print(z)
return 1
else:
print (z,'*', end=' ')
return (z * factorial_func(z-1))
z = 2000
print("The factorial of the given number", z," is as follows:")
print(factorial_func(z))Output:
So we can get the output to the factorial of 2000 by setting the recursion limit by 3000 using the sys module’s function setrecursionlimit().
Advantages and Disadvantages
Below are the different advantages and disadvantages of Recursive Functions in Python:
| Aspect | Advantages | Disadvantages |
| Simplicity | This often leads to more elegant and concise code. | It can be harder to understand for beginners. |
| Problem Suitability | A natural fit for specific problems like tree traversal and mathematical sequences. | It may not be the best choice for all problems. |
| Readability | It can make code more readable and self-explanatory for specific tasks. | Poorly structured recursion can be confusing. |
| Divide and Conquer | Ideal for divide-and-conquer algorithms. | Requires careful design of the base case. |
| Memory Consumption | It may consume more memory due to the call stack. | Risk of stack overflow for deeply nested recursion. |
| Performance | Performance may suffer compared to iterative solutions for some problems. | Iterative solutions can be more efficient. |
Conclusion – Python Recursion
Recursion is a handy solution for problems like tree traversal and other issues. Python is not a functional programming language, and we can see that the recursion stack is not that optimized compared to iteration. We should use iteration in our algorithm as it’s more optimized in Python and gives you better speed.
Recommended Articles
This is a guide to Python Recursion. Here, we define recursion in Python with different examples and differences between recursion and iteration, along with advantages and disadvantages. You can view EDUCBA’s recommended articles for more information.