PyTorch tanh

Updated April 5, 2023

Definition of PyTorch tanh

The hyperbolic tangent function also abbreviated as tanh is one of several activation functions. It is defined as, the hyperbolic tangent function having an average range of (-1, 1), therefore highly negative inputs are mapped to negative numbers.

What is PyTorch tanh?

PyTorch is a Facebook-developed open-source framework and machine learning library. Deep neural networks and natural language processing are two applications of it. Activation functions accept any integer as an input and convert it to an output. Researchers can employ nonlinear functions to achieve this goal because any function could be used as an activation function.

The following are characteristics of an ideal activation function:

• Nonlinearity — The activation function must be able to introduce nonlinearity in neural networks, particularly in hidden layer neurons. This is because straight connections are hardly used to illustrate real-world circumstances.
• Differentiable Activation Function – The activation function must be discrete. The network can learn by back-propagating loss from the output nodes to hidden units during the training stage. The backpropagation technique adjusts the weights of neurons in hidden layers using the derivative of their activation functions to reduce error in the following training period.

PyTorch tanh method

The most widely used activation functions are included in the Pytorch library. Layers (or classes) and definitions are provided for these activation functions (or functions). Tanh is a scaled sigmoid that has the same problems with gradient as the original sigmoid function. Model difficulties with vanishing gradient problems can be mitigated by varying weights.

Pytorch tanh is divided based on the output it produces i.e between -1 and 1 respectively. At every point, the hyperbolic tangent feature may be differentiated, and its derivative is 1 – tanh2(x). Because the expression uses the tanh function, the return of that function can be utilized to speed up reverse propagation. Tanh is similar to Sigmoid except that it is centered and ranges from -1 to 1. The function’s result will have a zero mean. As a result, the system will converge more quickly. It’s worth noting that if the mean of each input parameter is near 0, divergence is probably quicker. Batch Normalization is an example.

The class goes like this:

Class torch. nn. Tanh

The entity-wise hyperbolic tangent will indeed be generated if the input comprises several items.

torch. tanh (x, out=None)

Here, x: name of the input tensor

(optional): name of the output tensor

Tensor of the same type as x as the return type.

Tanh Activation Function Benefits

Tanh’s activation function is non-linear and discrete, both of which are desirable properties for an activation function. An activation function is defined as

class ActivationFunction(nn.Module):
def __init__(self):
super().__init__()
self.name = self.__class__.__name__
self.config = {"name": self.name}

It could be used to convert the outputs of a neuron to a negative number because its output varies from +1 to -1.

tanh(x)=(exp(x)-exp(-x))/(exp(x)+exp(-x))

class Tanh(ActivationFunction):
def forward(self, x):
x_exp, neg_x_exp = torch.exp(x), torch.exp(-x)
return (x_exp - neg_x_exp) / (x_exp + neg_x_exp)

Tanh Activation function for the free Forward Neural Network.

Here the Hidden layers with linear and non-linear are depicted. The Output shows no. of iteration, hidden layers and Accuracy.

import torch
import torch.nn as nn
import torchvision.transforms as transforms
import torchvision.datasets as dsets
train_dataset = dsets.MNIST(root='./data',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = dsets.MNIST(root='./data',
train=False,
transform=transforms.ToTensor())
class FeedforwardNeuralNetModel(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(FeedforwardNeuralNetModel, self).__init__()
self.f1 = nn.Linear(input_dim, hidden_dim)
self.tanh = nn.Tanh()
self.f2 = nn.Linear(hidden_dim, output_dim)
def forward (self, x):
out = self.f1(x)
out = self.tanh(out)
out = self.f2(out)
return out

PyTorch tanh function

In PyTorch, the function torch.tanh() supports the hyperbolic tangent function. The inputs must be in radian type, and the result must be in the range [-∞,∞]. Well here the input is a tensor, and if there are several elements in the input, entity hyperbolic tangential is generated. The Tanh() activation function is loaded once more using the nn package. Then, to obtain the result, random data is being generated and transferred.

Tanh function is called by

import torch.nn
tanh = nn.Tanh()
input = torch.randn(2)
output = tanh(input)

Let’s see sample code here:

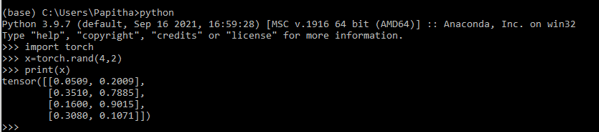
import torch
x=torch.rand(4,2)
print(x)

Output:

And lastly, we’ll illustrate each activation function in the following diagram to gain a better grasp of what they perform. The gradient of the function, in addition to the actual activation value, is a significant factor for optimizing the neural network. We can calculate the gradients in PyTorch by invoking the reverse function.

PyTorch tanh Examples

Below are the different examples:

Example #1

Code:

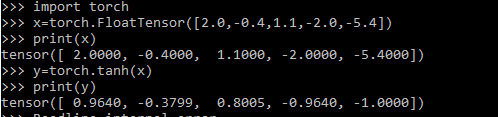
import torch
x=torch.FloatTensor([2.0,-0.4,1.1,-2.0,-5.4])
print(x)
y=torch.tanh(x)
print(y)

Output:

Example #2

Code:

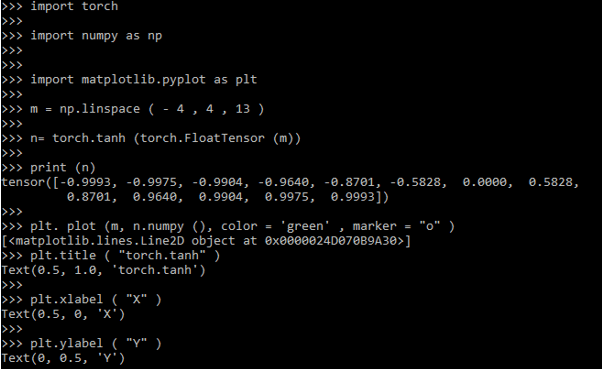
import torch
import numpy as np
import matplotlib.pyplot as plt
m = np.linspace ( - 4 , 4 , 13 )
n= torch.tanh (torch.FloatTensor (m))
print (n)
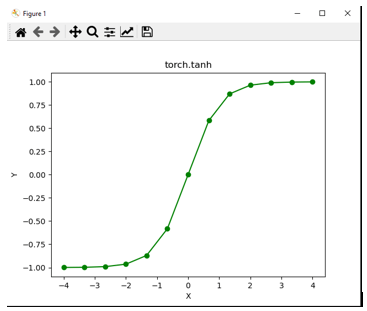
plt. plot (m, n.numpy (), color = 'green' , marker = "o" )
plt.title ( "torch.tanh" )
plt.xlabel ( "X" )
plt.ylabel ( "Y" )
plt.show ()
print (n)
tensor ([-0.9993, -0.9975, -0.9904, -0.9640, -0.8701, -0.5828, 0.0000, 0.5828, 0.8701, 0.9640, 0.9904, 0.9975, 0.9993])

Explanation

The above code is a visualization concept which imports Numpy and Pytorch Library and matplotlibrary is used for plotting tanh values. Here the vector size is 13 and ranges from -4 to 4. Finally, a plot is build which is shown in the below graph.

Output:

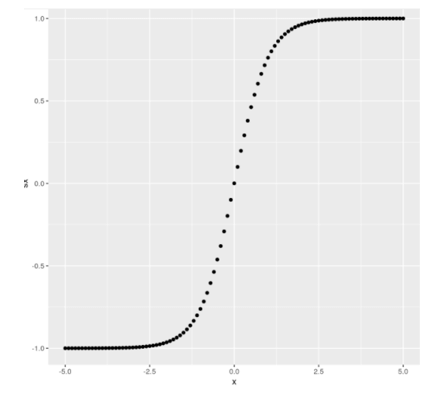
Example #3: Activation function tanh() using R

Code:

library(rTorch)
library(ggplot2)
a <- torch$range(-4., 4., 0.2)
b <- torch$tanh(a)
dfr <- data.frame(a = a$numpy(), sx = a$numpy())
dfr
ggplot(dfr, aes(a = a, b = sx)) +
geom_point() +
ggtitle("tanh")

Output:

Example #4

Code:

import numpy as np
import torch
data = [1.2, -3.2, 4.3, 0.5, -0.6, -1.8]
def tanh(x):
lists = list ()
for j in range(len(x)):
lists.append((np.exp(x[k]) - np.exp(-x[k])) / (np.exp(x[k]) + np.exp(-x[k])))
return lists
def tanh_derivative(x):
return 1 - np.power(tanh(x), 2)
out = [round (value, 3) for value in tanh(data)]
print (" Result of numpy tanh:", out)
print ("Result of numpt tanh derivative:", [round (value, 3) for value in tanh_derivative(data)])
print ("result of derivative2:", [round(1. - value*value, 3) for value in tanh(data)])
input = torch.FloatTensor(data)
a = torch.nn.Tanh()
out2= m(input)
print("pytorch tanh:", out2)
print("pytorch tanh derivative:", 1. - output2*output2)

Explanation

Pytorch Implementation is shown above and the result is given as:

Output:

Conclusion

As a result, we were able to understand how to utilize tanh() in PyTorch and its derivatives using straightforward explanations and code examples.

Recommended Articles

We hope that this EDUCBA information on “PyTorch tanh” was beneficial to you. You can view EDUCBA’s recommended articles for more information.

1. PyTorch CUDA
2. PyTorch Detach
3. pytorch gan
4. PyTorch Flatten