Updated April 6, 2023
Introduction to Prolog write
Prolog write is defined as, ‘write’ is an in-built predicate in prolog, it returns all the information that we required to show in the output, it gives clear output that means if we required output related to the program and with something friendly then we can use write predicate in the program, it uses terms to the current output by using appropriate brackets and operators, and that can be called as ‘write(Y)’ in which it writes the term Y to the current output stream, the stream is a continuous window with code writer, if an argument is a string, then it prints the string without quotes.
Syntax:
The syntax for ‘write’ in prolog will be as given below:
"write ('Enter the file name')." :Here, the ‘write’ predicate will show the output as it is from the bracket but without quotes.
"write(+Stream, +Term)" :We can read it as writing the term on the output stream. In this case, we need to call the ‘write’ by putting inputs.
Where,
o Term – It is a term that will be shown in the current output.
o Stream – It is a window or console where the output can be seen.
How write work in prolog?
The ‘write’ is a predefined in-built predicate in prolog, in which the terms are operated and also we can see the output in user-friendly notations that means user can understand the use of notation. This can also written as ‘write/1’. We can also use two write/1 commands, one after the other.
The working of built-in predicate write/1 is as following, it taking terms and that will print on the screen with user-friendly notations so that user can understand it.
For example,
o write(8+9+7).
output is :
8+9+7
yesIt gives the output as we use in terms.
o write(+(4,1)).
output is :
4+1
yesThe above query will give output as shown above.
o write([m+n+o]).
Output is :
[m+n+o]
yes
o write(.(u,.(v,[]))).
Output is :
[u,v]
yesIf we want elements to be arranged in a user-friendly format then we can follow the above examples as per the needs.
Now we will see when it will returns the contains variables,
o write(D).Output:
_26
yes
As above when we call the variable it will return the contains variable with its value prefix with _(underscore).
o E = d, write(E).Output:
d
E = d
yes
This is a case where we can give values to the term, here we given the value to the E and that will also be shown in the output because it contains the variable.
Let us see how to use two write/1 commands in prolog,
o write(m),write(n).Output:
mn
yes
In this case, we can say that prolog allow to writes two ‘write’ commands one after the other and the output is continuous, which means it will not take space or comma automatically.
o write(m),write(' '),write(n).Output:
m n
yes
In this case, we put write(‘ ‘) to print the space between two letters that are m,n, because when we write commands one after the other then it will automatically print one after the other means it will not take space so that we need to tell prolog to print space as ‘write(‘ ‘)’.
o write(m),write(' '),write(n).Output:
m n
yes
In this case, we have given 5 spaces between two letters. It means that we can put more than one space but we have to tell that to prolog to print it.
o write(p),tab(6),write(q).Output:
p q
yes
In this case, we can give space by using tab predicate. If we want six spaces in between the two letters then we can use tab predicate but we have to give arguments to it, which means if we want 6 spaces then pass argument 6 in tab.
o write(i),nl,write(j).Output:
i
j
yes
In this case, we used ‘nl’ predicate to break the line, ‘nl’ is a formatting predicate that tells to prolog to break the line and to go on printing on the next line. This is also a useful predicate in prolog.
The working of the ‘write’ predicate depends on the query and we can prepare queries per the requirements, so that as we have seen above many different types of examples with their outputs and the working of ‘write’ is very friendly and user can easily understand it.
Example #1
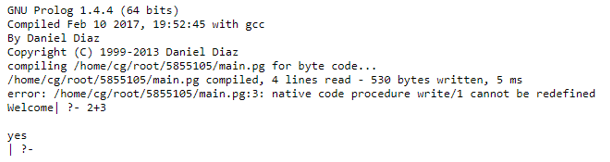
:- initialization(main).
main :- write('Welcome').
write(d+e+f).Input:
1) write(d+e+f).
2) write(+(2,3)).
3) write(.(5,.(6,[]))).
Output :
In the above program, at first ‘write’ predicate in the second line shows the quoted information in the output window that is automatically called while compiling. And in the third line, we use ‘write’ with the term ‘(d+e+F)’ but we need to call it by giving input. In this case, we give the input as ‘write(d+e+f).’, then it provides output as a term used.
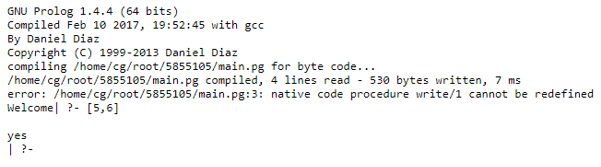
When we give the input ‘write(+(2,3)).’ then the output will be:
When we give input ‘write(.(5,.(6,[]))).’ then output will be:
Example #2
:- initialization(main).
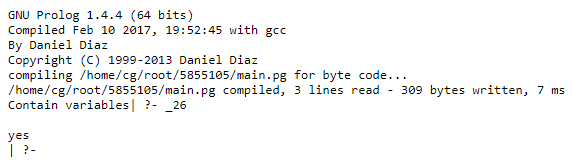
main :- write('Contain variables').Input:
1) write(A).
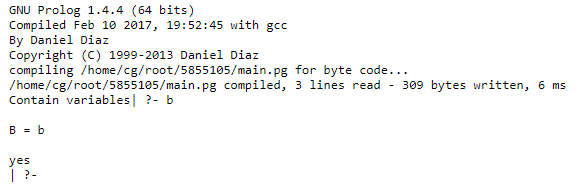
2) B = b, write(B).
Output:
In the above program, we called the ‘write’ predicate by giving input that is ‘write(A).’ then it gives output as it contains variables if we using the term as in capital letters then it will return the contains variables but if we put term as lowercase ‘a’ as an input then the output is ‘a’ itself.
When we give input as ‘B = b, write(B).’ then the output will be given below:
that means it will show the output as we put the values to its.
Conclusion
In the above article, we conclude that there are many predicates available in prolog out of that the ‘write’ is also a predefined predicate which is used to return the output as per the operations and defining as we see above and we can also conclude that above predicate is also useful to show program-related information in output.
Recommended Articles
We hope that this EDUCBA information on “Prolog write” was beneficial to you. You can view EDUCBA’s recommended articles for more information.