Updated April 6, 2023
Introduction to Prolog Factorial
Prolog factorial consists of two clauses. First is a unit clause with nobody and the second is a rule, which is with the body. Prolog programming is a logical and declarative programming language. Prolog name itself is shorter for PROgramming in LOGic, it includes research on theorem proofs and other deduction systems developed in the 1960s and ’70s. Prolog is one of the major examples of 4th generation programming language which supports the declarative paradigm. As the Japanese announced its 5th generation in 1981, had adopted programming as a development language. Let us see how Prolog factorial is designed and check out the actual logic behind factorial in prolog with few examples.
Logic behind Prolog
Prolog Factorial is the product of an integer and the other integers below the given number i.e., 5! is represented as 5*4*3*2*1 which is equal to 120.
Here in Prolog factorial,
- Prolog Factorial function definition is also similar to a normal factorial function.
- Factorial(0,1) i.e., factorial of 0 is generally 1.
- Factorial(N,M), if any temporary value N1 is assigned to N-1.
- Factorial(N1,M1), and is factorial of N1 is M1.
- M is NM1 i.e., assigning M to N*M1, then value of N is M.
- The above happens to be the recursive relation between N and factorial M. It reviews rules for particular relation in the top to bottom order.
Factorial Code:
factorial(0,1).
factorial(N,M) :-
N>0,
N1 is N-1,
factorial(N1, M1),
M is N*M1.- Also have two factorial definitions, they consist of two clauses.
- First clause is unit class with no body and the second clause is a rule as it has a body.
- Body of the second clause is on to the right side of ‘:-’ which is read as ‘if’.
- Body consists of literals separated by commas, each read as ‘and’.
- Head of clause is the total clause is clause is unit clause, else head of clause is part of clause appearing to the left of colon.
- Declarative reading of the first clause i.e. Factorial of 0 is 1 and the second clause declares Factorial of N is M if N>0 and N1 is N-1.
- Hence factorial of N1 is M1 and M is N*M1.
Consider an example to calculate factorial of 4 responds to value of W i.e., goal variable 8.
Will go with a clause tree to calculate the factorial of literate ‘factorial(4,W)’. As the clause tree does not contain any variable but has instances of variables. Branching of each node is determined by clause in the original program, using the relevant instances of variables.
Node is determined by some instance of head of the clause and the body literals of clause will determine node children in the clause tree.
Factorial(4,24)
4>0 3 is 4-1 factorial (3,3) 24 is 4*6
3>0 2 is 3-1 factorial(2,2) 6 is 3*2
2>0 1 is 2-1 factorial(1,1) 2 is 2*1
1>0 0 is 1-1 factorial(0,1) 1 is 1*1
TRUE
In this way, factorial of 4 being 24 is TRUE.
Examples of Prolog Factorial
Given below are the examples mentioned:
Example #1
Prolog factorial for 3!
Code:
factorial(0, 1).
factorial(N, M) :- N > 0, Prev is N -1, factorial(Prev, M1), M is M1 * N.
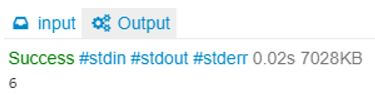
:- factorial(3,W), writeln(W).Output:
As the factorial of 3 will be 3*2*1 i.e., 6.
Example #2
Prolog Factorial for 4!
Code:
factorial(0, 1).
factorial(N, M) :- N > 0, Prev is N -1, factorial(Prev, M1), M is M1 * N.
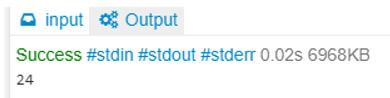
:- factorial(4,W), writeln(W).Output:
So here the 4! will be 4*3*2*1 i.e., 24.
Example #3
Prolog factorial for 10!
Code:
factorial(0, 1).
factorial(N, M) :- N > 0, Prev is N -1, factorial(Prev, M1), M is M1 * N.
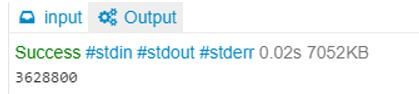
:- factorial(10,W), writeln(W).Output:
So here the 10! will be 10*9*8*7*6*5*4*3*2*1 i.e., 3628800.
Example #4
Prolog factorial for 1!
Code:
factorial(0, 1).
factorial(N, M) :- N > 0, Prev is N -1, factorial(Prev, M1), M is M1 * N.
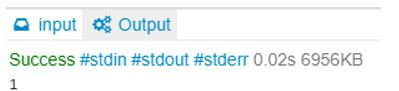
:- factorial(1,W), writeln(W).
Output:
So here, the factorial of 1 is 1.
It is calculated in very simple steps, as shown above. As we had seen earlier, in the factorial tree, all node children are true on evaluation, and the lowest one in tree corresponds to the first clause of the program. First clause can be written as, factorial(0,1) :- true.
Factorial(4,24) is consequence of Prolog program as there is a clause tree rooted and all of the root nodes are true, whereas literal factorial(5,6), on the other hand, is not at all a consequence of prolog program as there is no clause tree rooted for (5,6) and hence it gives false.
Conclusion
With this, we shall conclude the topic ‘Prolog Factorial’. We have seen what Prolog factorial and its definition is. We have gone through how Prolog word came from and what is the Prolog programming all about. We have seen a few of the examples too which give us the factorial of any non-negative integer. We have also depicted an example of 4! i.e., 24 being true with a clause tree, and also seen the logic involved with it.
Recommended Articles
We hope that this EDUCBA information on “Prolog Factorial” was beneficial to you. You can view EDUCBA’s recommended articles for more information.