Updated March 6, 2023

Introduction to Priority Queue
Priority queues are a special case of the queues where the elements are assigned the priorities according to requirement and further the operations are carried out depending on the priority of that particular element. In case, if more than one element inside the queue get the same priority then the serving or operations are carried out depending on the order in which they are placed inside the queue.
In most cases, the priority queues are implemented in such a way that the value of that particular element itself acts as the priority parameter for it or is further manipulated to assign the priority. In this article, we will study the working of priority queue, how we can implement the priority queues using the C programming language, and also discuss the time complexity required to carry out the priority queue implementation.
Functions of priority Queue
The working of the priority queue is the same as that of normal queues where we perform operations like search (peek), insert, and delete some elements from it. The only difference is the selection of the element while deletion. Instead of the first element which is inserted, the highest priority element is selected for deletion. Consider the queue shown in the below figure –
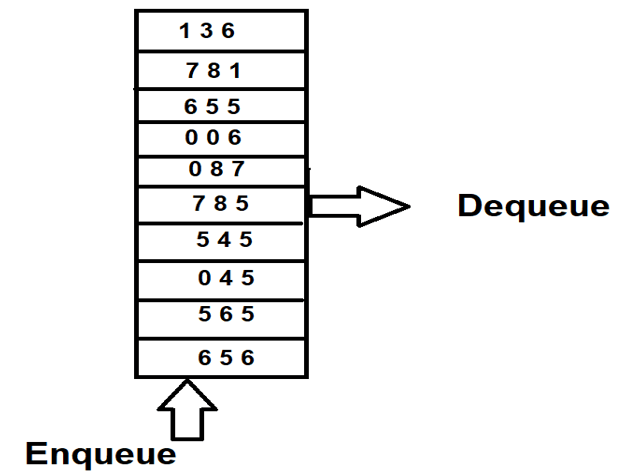
We can observe that from the one end the values are inserted in the queue pointed by enqueue but the dequeue operation will be carried out on the highest priority element. In the above figure, the element with the largest value has the highest priority, hence, 785 elements will be the first ones to be deleted from the priority queue.
The priority queue can be worked out by using Binary heap, binary search tree, and linked list. The time complexities for each of the operation in each of the case is as shown in the below table. It is upon your requirement that which operation is most frequently carried out on queue on the basis of which you can decide which data structure to be used for implementing priority queues-
| Operations | Binary Heap | Linked List | Binary Search Tree |
| Insert | O (log n) | O (n) | O (log n) |
| Peek | O (1) | O (1) | O (1) |
| Delete | O (log n) | O (1) | O (log n) |
Implementation of priority queue using the C programming language:
The following C program implements the priority queue by using the max-heap data structure and arrays.
// C program for implementing priority queue
#include <stdio.h>
int length = 0;
void swapTwoValues(int *item1, int *item2) {
int dummyItem = *item2;
*item2 = *item1;
*item1 = dummyItem;
}
// Prepare the heap for rerrangement of elements to carry out prepareHeap process
void prepareHeap(int array[], int length, int i) {
if (length == 1) {
printf("There is only one element in the Queue.");
} else {
// Detect the nodes which have the biggest value and its left and right child nodes.
int biggest = i;
int l = 2 * i + 1;
int r = 2 * i + 2;
if (l < length && array[l] > array[biggest])
biggest = l;
if (r < length && array[r] > array[biggest])
biggest = r;
// swapTwoValues and continue prepareHeaping if root is not biggest
if (biggest != i) {
swapTwoValues(&array[i], &array[biggest]);
prepareHeap(array, length, biggest);
}
}
}
// Function to addElement an element into the tree
void addElement(int array[], int newNumber) {
if (length == 0) {
array[0] = newNumber;
length += 1;
} else {
array[length] = newNumber;
length += 1;
for (int i = length / 2 - 1; i >= 0; i--) {
prepareHeap(array, length, i);
}
}
}
// Deletion of a particlar element from the array of max-heap tree
void rootDeletion(int array[], int number) {
int j;
for (j = 0; j < length; j++) {
if (number == array[j])
break;
}
swapTwoValues(&array[j], &array[length - 1]);
length -= 1;
for (int i = length / 2 - 1; i >= 0; i--) {
prepareHeap(array, length, i);
}
}
// Display the contents of array
void displayArray(int array[], int length) {
for (int i = 0; i < length; ++i)
printf("%d ", array[i]);
printf("\n");
}
// Controller of the program which calls different functions for manipulation
int main() {
int array[10];
addElement(array, 3);
addElement(array, 4);
addElement(array, 9);
addElement(array, 5);
addElement(array, 2);
printf("The contents of the max-heap array are : ");
displayArray(array, length);
rootDeletion(array, 4);
printf("The contents of the array after deleting one element from it: ");
displayArray(array, length);
}
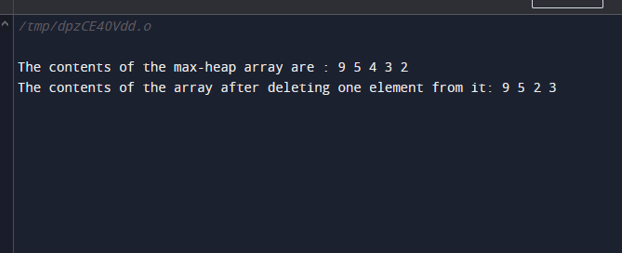
The output of the above C program is as shown below displaying all the contents of the max -heap and also the updated contents after deleting one of the elements. The above program demonstrates the implementation of all three operations on the priority queue which are insertion, searching, and deletion. We can observe that while deleting the element from the priority queue it was the element with the highest priority that got deleted in this case the largest value element. While in m=normal queue the FIFO pattern which says that the first inserted element should be the first one to remove is not followed in case of priority queues.
Time complexity
The time complexity of the priority queue, when implemented by using the above manner of using heap tree that is max-heap and the arrays, turns out to be O(n) where n is the number of elements. In the above example, the value of n is 5, hence, the complexity of time is O(5). The auxiliary space that is required is O(1).
Conclusion
The priority queue is just like a normal queue which performs enqueue a d dequeue operations to perform insertion or deletion of the element just the change is in the manner in which the value is selected for deletion. In the case of a normal queue, the FIFO pattern is followed which stands for the first in the first out format while deleting. In priority queues the elements are provided priorities according to the requirement like smallest element can be given highest priority or largest element can be given maximum priority. The element with the maximum priority is the first one to be chosen for deletion and then the next highest priority element and so on.
Recommended Articles
This is a guide to Priority Queue in Data Structure. Here we discuss the introduction, functions of priority Queue example with code implementation. You may also have a look at the following articles to learn more –

