Updated March 14, 2023
Introduction to PostOrder Traversal without Recursion
PostOrder Traversal without Recursion is a traversal method, where the left subtree is visited first, then right sub tree, and finally root node. Unlike array and linked lists, being linear data structures, we have several ways of traversing binary tree due to its hierarchical nature. It is also known as Iterative PostOrder Traversal, which is used to delete nodes in a Binary tree.
PostOrder Traversal without Recursion is more complex than InOrder and PreOrder Traversals, but PostOrder can be easily done using two stacks. Traversing Binary tree involves iterating over all the nodes of Binary Tree in a manner. As trees are not a part of linear data structure, there can be a possibility of more than 1 possible next node from a given node.
Syntax:
PostOrder Traversal does not have a particular syntax, but it is just the way users code, i.e., Algorithm or the Flowchart.
Algorithm of PostOrder Traversal without Recursion
To create an empty stack.
Follow the below steps while the root node is not NULL.
- Push the root node’s right child node to stack and then the root node.
- Set root node as root node’s left child node.
Pop one item from the stack and set it as the root node.
- If the item popped from the stack has a right child node and a right child node at the top, then the right child node is removed from the stack. Push the root node back and set the root node as the root node’s right child node.
- Else print the root node’s value and set the root node to NULL.
Repeat these steps until the stack is empty.
Let us consider an example and use PostOrder Traversal without Recursion using 1 Stack.
How PostOrder Traversal is Done?
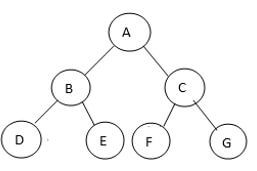
For the above example, we shall do a manual Postorder Traversal without Recursion.
Step 1: As the right child of A exists, C will be pushed to the stack and then A.
Stack: C, A
Move to the left child now.
Step 2: As the right child of B exists, E will be pushed to the stack and then B.
Stack: C, A, E, B
Move to the left child now.
Step 3: As the right child of D does not exist, D will be pushed to the stack.
Stack: C, A, E, B, D
Move to left child.
Step 4: As the current node is NULL, pop out D from the stack and, as the right child of D, does not exist. Set the current node to value NULL.
Stack: C, A, E, B
Step 5: As the current node is NULL, pop out B from the stack, and as the right child B equals the top element in the stack, pop out E from the stack and push B to the stack.
Stack: C, A, B
Step 6: As the right child of E does not exist, move E to stack and move to the left child.
Stack: C, A, B, E
Step 7: As the current node is NULL, pop out E from the stack and as the right child of E does not exist, print E and set the current node to NULL.
Stack: C, A, B
Step 8: As the current node is NULL, pop out B from the stack. As the right child of B is not equal to the top element in the stack. Print out B and set the current node to value NULL.
Stack: C, A
Step 9: As the current node is NULL, pop out A from the stack. As the right child of A equals the top element stack, pop out C from the stack, push A to the stack, and move the current node to the right child of A, i.e., C.
Stack: A
Step 10: Repeat the above steps and print out F, G, and C. Pop out A and print it out.
Example of PostOrder Traversal without Recursion
Given below is the example of PostOrder Traversal without Recursion:
Now, let us implement it using any programming language.
PostOrder Traversal without Recursion using Java.
Code:
import java.util.Stack;
class PostOrderNode
{
int val;
PostOrderNode leftNode, rightNode;
public PostOrderNode(int keyVal)
{
val = keyVal;
leftNode = rightNode = null;
}
}
class Main
{
public static void iterativePostOrder (PostOrderNode rootNode)
{
Stack<PostOrderNode> stack = new Stack();
stack.push(rootNode);
Stack<Integer> out = new Stack();
while (!stack.empty())
{
PostOrderNode currentNode = stack.pop();
out.push(currentNode.val);
if (currentNode.leftNode != null) {
stack.push(currentNode.leftNode);
}
if (currentNode.rightNode != null) {
stack.push(currentNode.rightNode);
}
}
while (!out.empty()) {
System.out.print(out.pop() + " ");
}
}
public static void main(String[] args)
{
PostOrderNode rootNode = new PostOrderNode(25);
rootNode.leftNode = new PostOrderNode(35);
rootNode.rightNode = new PostOrderNode(45);
rootNode.leftNode.leftNode = new PostOrderNode(55);
rootNode.leftNode.rightNode = new PostOrderNode(65);
rootNode.rightNode.leftNode = new PostOrderNode(75);
rootNode.rightNode.rightNode = new PostOrderNode(85);
iterativePostOrder(rootNode);
}
}
Output:
Here, as per the program, only one stack is being used, and postorder traversal is done without any recursion, i.e., iterative mode.
Conclusion
With this example, we have got to know How PostOrder traversal is done without recursion, i.e., in an iterative manner. We can now conclude the topic “PostOrder Traversal without Recursion”. We have seen what PostOrder traversal is and how is it implemented with a live example, solved manually. We have also seen Java programs written for PostOrder Traversal without any recursion, in an iterative manner using Stack.
Recommended Articles
This is a guide to PostOrder Traversal without Recursion. Here we discuss the introduction, algorithm and example, respectively. You may also have a look at the following articles to learn more –