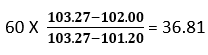Updated July 25, 2023
Introduction to Option Adjusted Spread
Option Adjusted spread (OAS) is a flat spread that has to be added to the treasury curve to make the theoretical price of an interest rate derivative equal to the market price by using dynamic pricing models that consider embedded options.
This is the measure of spread over government treasury bond yields when all the options have been considered. It is applied in MBS, CDO, Convertible debentures, and bonds with embedded options.
Formula
It’s useful for option-free bonds but not for an embedded option.
Option adjusted spread is used to measure the impact of optionality in the bond. It explicitly removes the value of an embedded option, giving a spread for the option-free bond. It is defined as follows:
For callable bonds, the issuer holds the right to buy back the bond at a call price (which is prespecified at the time of issue). If interest rates go down and the bond market price increases, the issuer has a right to redeem the bond at the call price, which is less than the prevailing market price giving benefit to the issuer. Option cost in this > 0 and hence OAS < Z.
For putable bonds, the option benefits the bond owner; it allows them to sell back the bond at a higher price to the issuer if the interest rate goes up and the prevailing price goes down. Hence Option cost is < 0 as OAS > Z.
Example of Option Adjusted Spread
Let’s explain this by taking an example:
Suppose the market price of a bond is $102, and the price calculated using the treasury curve is $103.27. Now we choose a 60 basis point parallel shift in the treasury zero curves that give us the price of $101.20, less than the market price of $102. We need to decrease the Treasury zero curve to equate the model price to the bond market price, i.e., the parallel shift will be somewhere between 0 and 60 bp. A series of iterations determines a parallel shift in the treasury curve that causes the model price to be equal to the market price.
Using linear interpolation, we get the below result:
On our second trial, we use a 36.81 basis point that gives a bond price of $101.95, approximately equal to the bond’s market price.
OAS Spread will be slightly less than the 36.81 calculated above.
Type of Spreads
- Nominal Spread: The difference between the Yield to maturity of the risky bond and the Yield to maturity of the risk-free bond (Treasury bond, which is assumed to be risk-free). The bond’s market price is obtained by adding the rate to the treasury par curve. Alternatively, we can say that the future stream of bond cash flows is discounted at the rate, representing the yield to maturity (YTM). It is a poor measure as it ignores the term structure of the interest rate.
- Zero volatility: It spread (Z- Spread) is the single value-added to the treasury spot curve to give the discount rate that equates the bond’s present value to its current market price. This is done on a trial and error basis.
It is superior to nominal spread as it takes into the term structure of interest rate, which is ignored in the earlier approach. Let’s denote the Present value of the risky bond as PV, Rf as the risk-free rate, z as the spread, C as the future stream of cash flows, and FV as the bond’s future value, which includes a coupon to be paid.
Advantages of Option Adjusted Spread
Some of the advantages are:
- By separating bonds with an embedded option from its optionality feature, investors can determine whether the investment is worthwhile.
- OAS provides a more accurate picture of embedded option contracts than just comparing the yield of two bonds. It uses advanced models like Monte Carlo analysis in simulation.
- Reliable as the calculation is similar to that of the Z spread calculation. The OAS approach recognizes the security’s cash flows along each path, incorporating the optionality of cash flows into the analysis.
Disadvantages of Option Adjusted Spread
Some of the disadvantages are:
- Measurement is complicated because OAS is a very dynamic value, responding to changes in the level and shape of the yield curve, volatility, prepayments, credit spread, liquidity, etc.
- The assumption underlying OAS is that historical data will observe in the future.
- Regime changes necessitate updates to the OAS model as economic data shifts and become responsive to new conditions.
- Model dependent
- Difficulty in interpretation can result in a distorted picture of the behavior of securities.
Limitations of Option Adjusted Spread
Some of the Limitations are:
Portfolio OAS is usually calculated as a weighted average of OASs of component securities where weight is assigned based on the market price of securities. However, the greatest risk for an investor for embedded option bonds is a change in the interest rate and prepayment risk (which may lead to the early retirement of their investments before the scheduled period), so the weight assigned to the security should be a combination of duration and market price.
Important Points to Remember
Some of the Important points are:
- OAS will equal the Z spread for bonds with no embedded option.
- The difference between OAS and Z spread provides the implied cost of the embedded option.
- OAS utilizes multiple scenarios with various interest rate paths and levels calibrated to security yield curve to determine cash flows. Then the result is used in arriving at the price of a security.
- In option-embedded bonds, an option’s exercise depends on the interest rate’s volatility.
- Two Mortgage-backed bonds with the same estimated maturity but with two different OAS spreads will provide different returns, i.e., bonds with the higher OAS will be selling at a lower price than bonds with a lower OAS. Hence, investors should consider earlier bonds to maximize potential return.
Conclusion
Despite complex calculations and dependence on sophisticated models, OAS has become an analytical tool superior to traditional methods for evaluating embedded securities.
Recommended Articles
This is a guide to Option Adjusted Spread. Here we discuss the formula and example of option-adjusted spread along with advantages, disadvantages, and limitations. You may also look at the following articles to learn more –