Updated March 28, 2023
Introduction to numpy.mean()
Numpy.mean() is function in Python language which is responsible for calculating the arithmetic mean for the all the elements present in the array entered by the user. Simply put the functions takes the sum of all the individual elements present along the provided axis and divides the summation by the number of individual calculated elements. The axis along which the calculation is made has to be prespecified or else the default value for axes will be taken.
Syntax and Parameters
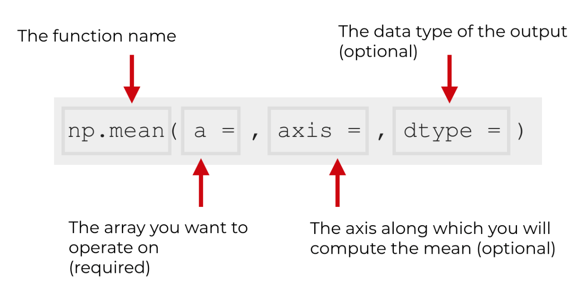
The following is the syntax that displays how to implement numpy.mean().
numpy.mean (a, axis =None, dtype = None, out = None, keepdims =<no value>) The syntax entered by the user is sent in terms of float * 64 intermediate and there by returns the value for the associated integers corresponding for the mean value.
The parameter used in the Syntax for using numpy.mean()
- a *: *array *_ *like *
The array is being entered by the user or prompted to be entered. In case the array entered is not of an integer data type, then the conversion of the form is tried on the data entered.
- axis : None *, * *int *, * *tuple * (optional parameter)
The computation of the axis along the elements of the specified array entered by the user is done. By default, the mean of the pre-flattened array is computed. In case the array entered is a tuple, in such a case the mean is computed over various axes of the array.
- dtype * *: * *data *– *type *, (parameter is optional)
For the computation of the mean the parameter type is utilized. By default, the float 64data type is used for arrays with integer data sets. In case the data being input is floating it remains the same as the dtype entered.
- out : ndarray, (parameter is optional)
It is an alternative array which is made to record the resultant mean. By default, the parameters stay None. In case it is provided the array is needed to have the same ascertained shape as that of the output which is expected.
- keepdims: bool, (parameter is optional)
If the parameter specified is True, the axis or axes which are deduced are kept in the expected result as the dimensions having size one. The option enables the result to be broadcasted correctly in response to the array which has been entered. In case value by default, a parameter is passed then the keepdims parameter would not be passed on to the method-specific for mean with respect to the array and its sub-classes. However, it must be noted that for non-default values passed the keepdims parameter would be applicable to raising exceptions if any.
- m : ndarray
If the parameter out=None, then in such a case a new array is returned which contains the mean values. Else, in such cases, the reference values with respect to the elements if retuned.
Example to Implementation NumPy.mean()
Below are the examples mentioned:
Code:
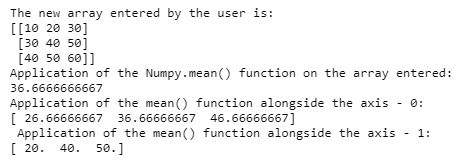
import numpy as n1
a1 = n1.array([[10,20,30],[30,40,50],[40,50,60]])
print 'The new array entered by the user is:'
print a1
print 'Application of the Numpy.mean() function on the array entered:'
print n1.mean(a1)
print 'Application of the mean() function alongside the axis - 0:'
print n1.mean(a1, axis = 0)
print ' Application of the mean() function alongside the axis - 1:'
print n1.mean(a1, axis = 1)The following output would be produced for the code specified above:
How Does the numpy.mean() Work?
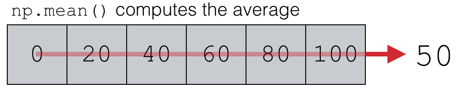
The function scans through the values which are specified in the array which is provided by the user. It firstly tries to flatten the resultant array before the computation of the arithmetic mean on the same. The below diagrammatic systemic representation shows the function actually executes the calculation:
We can use the NumPy mean function to compute the mean value:
- As the function for mean travels through various axis or axes provided by the user, it scan through and tries to integrate the arithmetic mean functionality for all integral values, Where the elements do not match up to be integral data type, it tries to convert such numbers.
- Here you can see for a single dimensional array with six specified elements, the functions scans each of the elements and then divides the total summation of the elements by the total number of elements present in the array (here 6).
- This way for arrays with multiple dimensions all or specified axis is mentioned along which the mean is calculated which is displayed in an array form for more than one-dimensional arrays.
Conclusion
The function mean() in NumPy is very useful for calculating the arithmetic average of elements especially in terms of data given in array subsets. This being calculated through manual code impacts the verbosity of the code and thus impacts on the computation time for long codes with large data sets.
Recommended Articles
This is a guide to numpy.mean(). Here we discuss the introduction and working of numpy.mean() along with different examples and its code implementation. You may also look at the following articles to learn more –