Introduction to numpy.sort
Numpy.sort() is a sorting function that helps in arranging the elements of an array in a certain order. Let’s say we want to sort our array in ascending order along the first axis, then numpy.sort() comes to our rescue. Numpy provides four different sorting algorithms: quicksort, heapsort, mergesort, and timsort. We will be discussing these algorithms in great detail while solving some examples. We can choose any of the mentioned algorithms based on the required time and space complexity.
Syntax and Parameters
Moving ahead, let’s discuss the numpy.sort() function in greater details. The standard syntax for writing this function is as follows :
numpy.sort(a, axis=-1, kind=None, order=None)The parameters of numpy.sort() are :
- a: array-like object – The input array to be sorted.
- axis: 0, -1 or none – The axis along which the array has to be sort. If nothing is mentioned, then the array is flattened before sorting. By default, the array is sorted along the last axis. It is denoted by axis = -1.
- kind: {‘quicksort’, ‘mergesort’, ‘heapsort’, ‘stable’} – In numpy, we can choose from any of these sorting algorithms {‘quicksort’, ‘mergesort’, ‘heapsort’, ‘stable’}. By default, the input array will be sorted by using quicksort.
- order: order of sorting {string or list} – This parameter specifies the field along which the sorting has to be done. It usually used when we have a field defined array.
Out of the above-mentioned parameters, the first parameter is compulsory. The other parameters are optional and can be used based on the specific requirement. The numpy.sort() function returns a sorted copy of the input array.
Examples to Illustrate numpy.sort
Following are the different examples to illustrate numpy.sort.
Example #1
Program to illustrate sorting along different axes using numpy.sort()
Code:
import numpy as np
#creating an array
A = np.array([[15, 1], [19, 94]])
print ("The input array is : \n", A)
# sorting along the first axis
A_sorted = np.sort(A, axis = 0)
print ("Sorted array along the first axis : \n", A_sorted)
#sorting along the last axis
A_sorted = np.sort(A, axis = -1)
print ("Sorted array along the last axis : \n", A_sorted)
#sorting the flattened axis
A_sorted = np.sort(A, axis = None)
print ("Sorted array when flattened: \n", A_sorted)Output:
Example #2
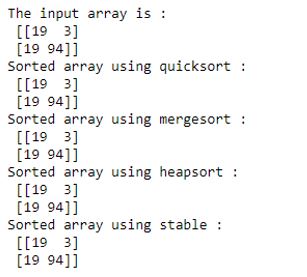
Program to illustrate sorting using different sorting algorithms using numpy.sort()
Code:
import numpy as np
#creating an array
A = np.array([[19, 3], [19, 94]])
print ("The input array is : \n", A)
# sorting along the first axis using quicksort
A_sorted = np.sort(A, axis = 0, kind = 'quicksort')
print ("Sorted array using quicksort : \n", A_sorted)
# sorting along the first axis using mergesort
A_sorted = np.sort(A, axis = 0, kind = 'mergesort')
print ("Sorted array using mergesort : \n", A_sorted)
# sorting along the first axis using heapsort
A_sorted = np.sort(A, axis = 0, kind = 'heapsort')
print ("Sorted array using heapsort : \n", A_sorted)
# sorting along the first axis using stable
A_sorted = np.sort(A, axis = 0, kind = 'stable')
print ("Sorted array using stable : \n", A_sorted)Output:
Quickly comparing the space and time complexity of different algorithms.
| Type of Analysis | Quicksort | Heapsort | Mergesort | timsort |
| Best Case | O(n*log(n)) | O(n*log(n)) | O(n*log(n)) | O(nk) |
| Worst Case | O(n^2) | O(n*log(n)) | O(n*log(n)) | O(nk) |
| Average Case | O(n*log(n)) | O(n*log(n)) | O(n*log(n)) | O(nk) |
| Space | Constant | Constant | Depends | Depends |
| Stability | No | No | Yes | Yes |
Stable in itself is not a sorting algorithm. It is a keyword used to direct the function to automatically choose the best stable sorting algorithm for the data type being sorted. In the current versions of numpy, it has been mapped to merge sort and radix sort. They are used alternatively based on the data type.
Quicksort and heapsort are in-place sorting algorithms. They do not require additional space for making comparisons. Whereas merge sort is an out-place algorithm. It requires O(n) space in arrays. So, you may choose any of these algorithms based on space constraints. Timsort is best for almost or already sorted arrays. If you do not mention the kind parameter in the function, then numpy.sort() will use quicksort by default.
Example #3
Program to illustrate sorting in a field defined or structured array using numpy.sort()
Code:
import numpy as np
#defining values and data type for creating a field defined array
dtype = [('student', 'S10'), ('weight', float),('height', float),('age', int)]
values = [('Jane',53.2,1.63,18), ('Janice',69.4,1.56,22),('Gartner',72.5,1.7,21),('Raul',70.5,1.5,21)]
# creating a field defined array
A = np.array(values, dtype=dtype)
print ("The input array is : \n", A)
# sorting the array by age
A_sorted = np.sort(A, order = 'age')
print ("Sorted array by age: \n", A_sorted)
# sorting the array by age then by height if age is equal
A_sorted = np.sort(A, order = ['age','height'])
print ("Sorted array by age and then by height: \n", A_sorted)
# sorting the array by age then by height and finally by weight if age and height are equal
A_sorted = np.sort(A, order = ['age','height'])
print ("Sorted array by age and then by height and weight: \n", A_sorted)Output:
Conclusion
Numpy.sort() is a sorting function used for arranging the elements of an array-like object. The function takes an array-like object as an input and outputs a sorted copy of the input array. In numpy, we can use four types of algorithms to sort the arrays. The algorithms are quicksort, heapsort, mergesort, and timsort.
There are a few other sorting functions in the numpy module, such as ndarray.sort()( to sort an array in-place), np.argsort() (for indirect sort), np.lexsort() (for indirect stable sort on multiple keys) and np.partition() ( for partial sort). We will be discussing them in greater detail in the coming posts.
Recommended Articles
This is a guide to numpy.sort. Here we discuss the Introduction and parameters of numpy.sort along with the examples and code implementation. You may also look at the following articles to learn more –