Updated April 15, 2023
Introduction to NumPy Identity Matrix
NumPy identity matrix is an inbuilt NumPy work that is utilized for restoring a framework, i.e., a 2D cluster having 1’s at its fundamental askew and 0’s somewhere else. The identity() work is characterized under NumPy, which can be imported as import NumPy as np, and we can make multidimensional exhibits and infer other numerical measurements with the assistance of NumPy. The identity cluster is a square exhibit with ones on the primary inclining. Python identity() work returns the personality exhibit. The number of lines (and sections) in n x n yield. Information sort of the yield.
Syntax and Parameters
NumPy.identity(dtype=None,n)Where,
‘n’ represents the number of rows and columns in the NumPy identity matrix.
Dtype represents the data type of the object, which is taken as afloat by default.
It returns a ndarray n x n cluster with its fundamental slanting set to one and all different components 0.
How does the NumPy identity matrix work?
Now we see various examples of how the NumPy identity matrix works in Python.
Example #1
Using NumPy identity matrix to find out the matrix values
Code:
import numpy as geek
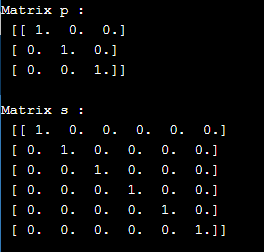
p = geek.identity(3, dtype = float)
print("Matrix p : \n", p)
s = geek.identity(6)
print("\nMatrix s : \n", s)Output:
In the above program, we first import the NumPy library as a geek and define the matrix s and p. After defining the matrices, we would like to print the matrix values, and that is the reason why we use the identity() matrix function to displace the matrix values the number of times we would have mentioned in the program. Hence, the program is implemented, and the output is as shown in the above snapshot.
Example #2
Using NumPy identity matrix to find the matrix values of multiple n*n arrays
Code:
import numpy as np
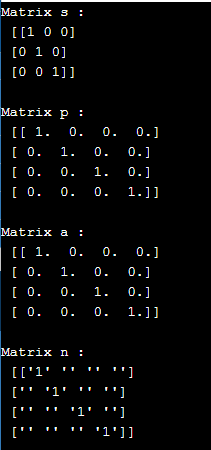
s = np.identity(3, dtype=int)
print("Matrix s : \n", s)
p = np.identity(4)
print("\nMatrix p : \n", p)
a = np.identity(4, dtype=float)
print("\nMatrix a : \n", a)
n = np.identity(4, dtype=str)
print("\nMatrix n : \n", n)Output:
In the above program, we have 2*2,3*3,4*4 matrices, and we import NumPy as np and implement the values of all these matrix values. Then we use the NumPy identity matrix to provide the values for the datatypes and finally implement the values based on the number of times given. Hence, the program is implemented, and the output is as shown in the above snapshot.
In the first capacity number of lines and sections was 2. In this way, a lattice of 2 X 2 was shown, having its principle askew with esteem 1 with return type as an int. Here, drift esteems were returned as character work has coast return type as a matter of course. In the second capacity number of lines was 3, and the section was 3. Along these lines, a network of 3 X 3 was shown, having its primary askew as 1 with return type as afloat.
In the third capacity number of lines was 3, and the section was 3, so a framework of 3 X 3 was shown, having its fundamental corner to corner as 1 with return type as a string. What’s more, different qualities were introduced to exhaust characters, which portray esteem equivalent to zero.
In the fourth capacity number of lines was 3, and the segment was 3. Thus, a grid of 3 X 3 was shown, having its primary slanting as 1 with return type as a string.
NumPy is a bundle for logical registering, which has upheld for an amazing N-dimensional exhibit object. NumPy gives a multi-dimensional cluster of numbers which is really an article. To increase the two frameworks, we use the speck() technique. Get familiar with how numpy.dot functions. * is utilized for cluster increase (augmentation of relating components of two exhibits), not lattice duplication. Comparative like records, we can get to network components utilizing a list. NumPy, which represents Numerical Python, is a library comprising of multidimensional exhibit objects and an assortment of schedules for handling those clusters. Utilizing NumPy, numerical, and intelligent procedures on exhibits can be performed.
Conclusion
Hence, I would conclude by stating that NumPy is the best libraries for doing complex control on the exhibits. It’s extremely simple to calculate exhibits utilizing the NumPy libraries. Cluster control is to some degree simple, yet I see numerous new apprentices or moderate designers discover challenges in lattices control. Transpose is another framework that results from when all the components of lines are present in the segment and bad habit – versa. You can discover the translation of a network utilizing the matrix variable T. Like, for this situation, I need to render the matrix 2. The framework is generally utilized by the information researcher for information control. After perusing this instructional exercise, I trust you can control the framework.
Recommended Articles
This is a guide to NumPy Identity Matrix. Here we discuss How does the NumPy identity matrix work along with the syntax and parameters. You may also have a look at the following articles to learn more –