Updated July 13, 2023
Definition of Nominal Rate of Return
The nominal rate of return (also known as the inflationary rate of return) is the rate of return required over the period of time after considering the present inflation rate prevalent in the economy, computed either using an addictive model or multiplicative model and such return is mostly used in confirming the viability of the proposed project or for discounting purpose.
Explanation
- Suppose you invest a sum amount in the bank & the rate of return is 7%. Such interest rate offered by banks does not cover the effect of inflation. If inflation is lower, the investors ignore the difference. However, if the inflation is higher, the investors take the difference on a serious note & avoid investing in safe deposits.
- That’s the difference between a real interest & inflation rate. So the difference between the two is inflation.
- An increase or decrease in inflation affects prices. The prices increase as a result of inflation. An inflation increase often treats as an increase in GDP growth percentage. Such an increase is short-term & the economy returns to equilibrium if the GDP growth is not sustainable.
- Thus, inflation is used in various finance disciples, and the list is never-ending.
The Formula for the Nominal Rate of Return
There are two methods for the computation of the nominal rate of return.
The method I: Addictive Method
Method II: Multiplicative Method
Explanation: The multiplicative model is widespread in the finance world. Obviously, the result from the multiplicative model results in a higher inflation rate than the addictive model. Then why do we use the multiplicative model? The reason is the compounding effect of the inflation rate. The inflation today was a multiplicative of inflation yesterday.
Example of Nominal Rate of Return (With Excel Template)
Let’s take an example to understand better the Nominal Rate of Return calculation in a better manner.
Example #1
Suppose a person has invested $ 450000 today in a fund. The return received after 1 year is $ 485600. We need to compute the nominal rate of return earned by the said person
Solution:
| Particulars | Amount ($) | |
| A | Amount of Investment | 450000 |
| B | Realization after one year | 485600 |
| C | Difference (B-A) | 35600 |
| D | Percentage Return (C/A)*100 | 7.91% |
Explanation: What we observe here is the rate of return earned. Can this be termed as a nominal rate of return? Absolutely yes. Here, 7.91% reflects the impact of the real interest rate plus the inflation prevalent in the economy.
Example #2
Let us take a classic example used worldwide:
Suppose a bond of the face value of $ 100,000 pays a coupon of 8% over the period of 5 years & redeemable at a 10% premium. The expected rate of return is 10%. The cash flows will be received in two installments during the year, i.e., half-yearly. The investor wants to know the “should be a price” of the bond today.
Solution:
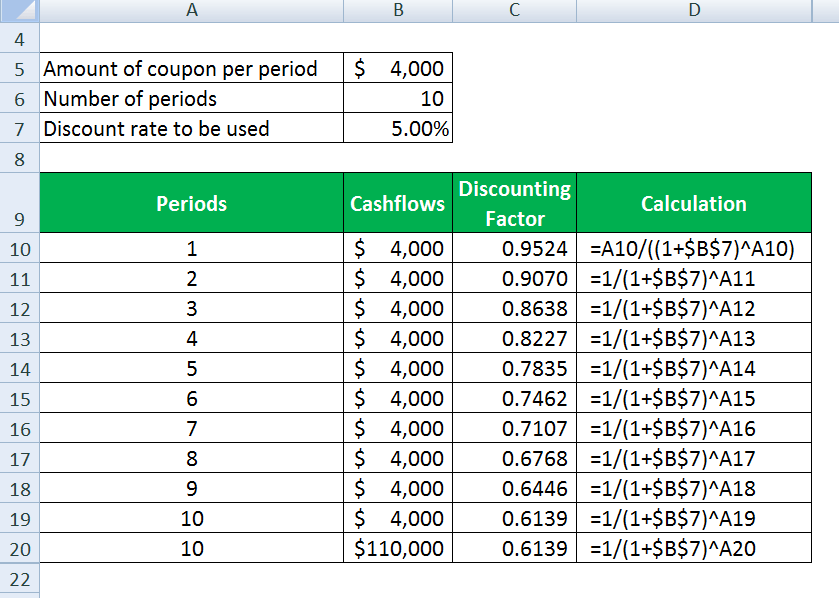
| Amount of coupon per period | $4,000 |
| Number of periods | 10 |
| Discount rate to be used | 5.00% |
Discounting factor calculates as
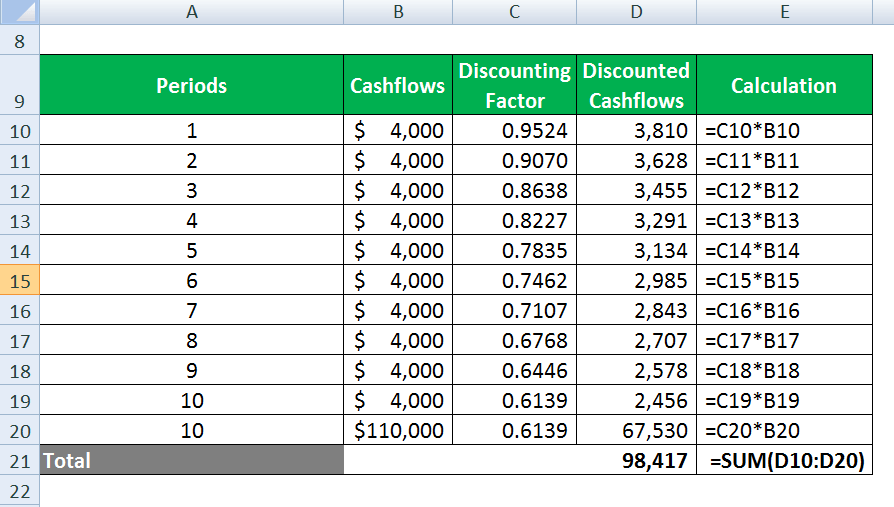
Discounted Cashflow calculated as
| Periods | Cashflows | Discounting factor | Discounted Cashflows |
| 1 | $ 4,000 | 0.9524 | 3,810 |
| 2 | $ 4,000 | 0.9070 | 3,628 |
| 3 | $ 4,000 | 0.8638 | 3,455 |
| 4 | $ 4,000 | 0.8227 | 3,291 |
| 5 | $ 4,000 | 0.7835 | 3,134 |
| 6 | $ 4,000 | 0.7462 | 2,985 |
| 7 | $ 4,000 | 0.7107 | 2,843 |
| 8 | $ 4,000 | 0.6768 | 2,707 |
| 9 | $ 4,000 | 0.6446 | 2,578 |
| 10 | $ 4,000 | 0.6139 | 2,456 |
| 10 | $ 1,10,000 | 0.6139 | 67,530 |
| Total | 98,417 |
Thus, the bond should be bought not higher than $ 98417 if he requires a return of 10% compounded semi-annually.
Explanation
- The required rate of return here is 10%. This rate includes inflation as well as the real interest rate.
- The bond will pay a flat coupon of $ 4000 per period. However, if the investor needs to have a higher rate of return. He needs to purchase the same bond at less than face value.
- The “should be” price computed above is compared with the actual price of the bond. If the actual price is higher, it is suggested that the investor should sell the bond now. If the actual price is lower than the fair value computed, it suggests buying the stock. In the worst case, if the actual price of a bond is very near to the price calculated above, it is suggested to hold the bond or do nothing.
- As you can see, the slightest change in the required return rate can change the bond decision.
Importance of Nominal Rate of Return
- The nominal interest is very important in the finance & economic world.
- It is necessary for computing various discounted values.
- The increase in the nominal rate progressively defines the increasing inflation rate in the economy.
- The whole economic base is related to the nominal rate of return. Therefore, many financial decisions are impacted due to a slight change in the nominal rate of return.
- Reduction in nominal rate results in higher output values & vice-versa.
Advantages
Some of the advantages are given below:
- It is used in discounting the cashflows standing at different intervals over the projected tenure of the project.
- Further, such a rate of return is used to compute the net present values of cash flows. The project is viable if the net cash flows can survive the effect of the nominal interest rate.
- Such interest rate is compared with the internal rate of return. The nominal rate of return is considered to cost of the project & such requirement is the minimum quantum of return. If the internal rate of return is lower than the nominal rate of return, the project is said to have reduced the wealth of shareholders & is, therefore, not viable to carry out.
Disadvantages
Some of the disadvantages are given below:
- It includes inflation & thus; the results are always inflation than the actual scenario.
- Firms need to think about the appropriate nominal rate. Any wrong basis in the rate may provide devastating results.
- The nominal rate of return has now become the only basis of decision-making in finance, ignoring the other disciples of finance.
- An important project may be rejected only due to negative NPV. Thus, other factors should be considered to confirm whether the project is not feasible.
Conclusion
The nominal rate of return is the backbone of the finance world today. Any computation in finance without an appropriate discount rate is considered vague & irrational. Thus, the nominal rate of return has gained much importance in the changing world of the economic environment.
Recommended Articles
This is a guide to the Nominal Rate of Return. Here we also discuss the definition and examples of the nominal rate of return and its advantages and disadvantages. You may also have a look at the following articles to learn more –