IIR Filter Matlab

Updated March 13, 2023

Introduction to IIR Filter Matlab

IIR filter is a type of digital filter used in DSP (Digital Signal Processing) applications; it is an abbreviation for “Infinite Impulse Response.” For the IIR filter, the response is “infinite” as there is feedback in this type of filter. For example, if we put an impulse, i.e. a single sample “1”, followed by several “0” samples, then we will get an infinite number of non-zero values. In this topic, we are going to learn about IIR Filter Matlab.

The advantage of IIR filters is that they can achieve the required filtering characteristics while utilizing lesser memory & performing fewer calculations as compared to a similar ‘Finite Impulse Response filter.

In MATLAB, we can design various IIF filters like Butterworth, Chebyshev, and Bessel.

Syntax of IIR Filter Matlab

The syntax for creating different types of IIR filters

1. [y, x] = butter(n, F)
2. [y, x] = cheby1(n, Fp, Rp)
3. [y, x] = besself(n, Fa)

Description:

1. [y, x] = butter(n, F) is used to return the transfer function coefficients for an nth-order digital Butterworth filter. This is a lowpass filter with a normalized cut off frequency of F
2. [y, x] = cheby1(n, Rp, Fp)  is used to return the transfer function coefficients for an nth-order digital Chebyshev I filter. This is a lowpass filter with a normalized passband edge frequency ‘Fp’& peak to peak passband ripple ‘Rp.’
3. [y, x] = besself(n, Fa) is used to return the transfer function coefficients for the nth-order analog Bessel filter. This is a lowpass filter with ‘Fa’ as angular frequency. This is the frequency till which the group delay of the Bessel filter is almost constant.

Examples of IIR Filter Matlab

Let us now understand the code for creating different types of IIR filters in MATLAB.

Example #1

In this example, we will create a Low pass Butterworth filter:

For our first example, we will follow the following steps:

1. Initialize the cut off frequency
2. Initialize the sampling frequency
3. For this example, we will create a Low pass Butterworth filter of order 5
4. Next, we will use the filter created in the above steps to filter a random signal of 3000 samples

Code:

F = 400

[Initializing the cut off frequency to 400]

Fs = 1000

[Initializing the sampling frequency to 1000]

[y, x] = butter(5, F/(Fs/2))

[Creating the Butterworth filter of order 5]

inputSignal = randn(3000, 1);

[Creating a random signal of 3000 samples]

outSignal = filter(y, x, inputSignal);

[Passing the input signal as an input to the Butterworth filter created]

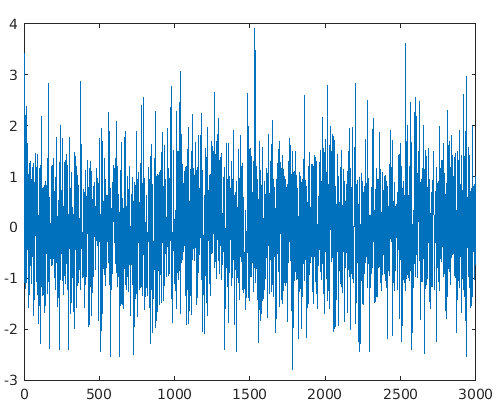
plot(outSignal)

[Plotting the output of the Butterworth filter]

Input:

F = 400
Fs = 1000
[y, x] = butter(5, F/(Fs/2))
inputSignal = randn(3000, 1);
outSignal = filter(y, x, inputSignal);
plot(outSignal)

Output:

As we can see in the output, using a low pass Butterworth filter, which is a type of IIR filter, we can filter the signal of 3000 random samples.

Example #2

In this example, we will create a Low pass Chebyshev filter (Type 1):

For this example, we will follow the following steps:

1. Initialize the passband ripple
2. Initialize the passband edge frequency
3. For this example, we will create a Low pass Chebyshev filter of order 4
4. Next, we will use the filter created in the above steps to filter a random signal of 3000 samples

Code:

n = 4

[Initializing the order]

Rp = 20

[Initializing the passband ripple to 20]

Fp = 0.3

[Initializing the passband edge frequency and sampling it by 1000]

[y, x] = cheby1(n, Rp, Fp);

[Creating the Type 1 Chebyshev filter of order 4]

inputSignal = randn(3000, 1);

[Creating a random signal of 3000 samples]

outSignal = filter(y, x, inputSignal);

[Passing the input signal as an input to the Chebyshev filter created]

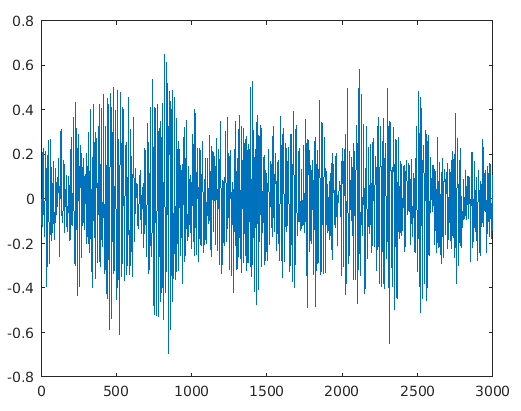
plot(outSignal)

[Plotting the output of the Chebyshev filter]

Input:

n = 4
Rp = 20
Fp = 0.3
[y, x] = cheby1(n, Rp, Fp);
inputSignal = randn(3000, 1);
outSignal = filter(y, x, inputSignal);
plot(outSignal)

Output:

As we can see in the output, using a low pass Chebyshev filter, which is a type of IIR filter, we can filter the signal of 3000 random samples.

Example #3

In this example, we will create a Low pass Bessel filter.

For this example, we will follow the following steps:

1. Initialize the order of the Bessel filter
2. Initialize the constant group delay
3. Next, we will plot the transfer function coefficients for the filter created in the above steps.

Code:

n = 4

[Initializing the order]

Fa = 100000

[Initializing the constant group delay to 100000]

[y, x] = besself(n, Fa);

[Creating the Bessel filter of order 4]

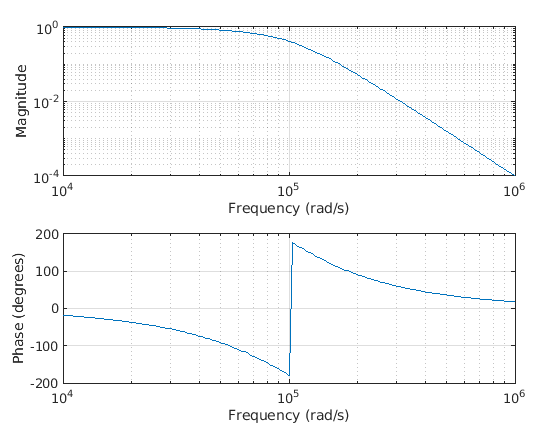
freqs(y, x)

[Plotting the coefficients of the transfer function of the Bessel filter]

Input:

n = 4
Fa = 100000
[y, x] = besself(n, Fa);
freqs(y, x)

Output:

As we can see in the output, we have obtained the magnitude and phase response for the Bessel filter, which is a type of IIR filter.

Conclusion

1. IIR filters provide infinite impulse response and are used to achieve the required filtering characteristic while utilizing lesser memory & performing fewer calculations
2. Butterworth, Chebyshev, Bessel are some types of IIR filter
3. In MATLAB, we can use commands like ‘butter’, ‘cheby1’, ‘besself’ to design different types of IIR filters

Recommended Articles

This is a guide to IIR Filter Matlab. Here we discuss the Examples of IIR Filter Matlab along with the codes and outputs. You may also have a look at the following articles to learn more –

1. Matlab Images
2. MATLAB Unique
3. Trapezoidal Rule Matlab
4. Curve Fitting Matlab