Introduction to Hierarchical Clustering
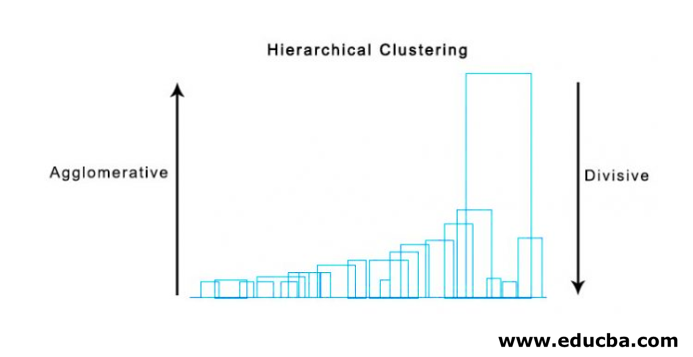
Hierarchical clustering is defined as an unsupervised learning method that separates the data into different groups based upon the similarity measures, defined as clusters, to form the hierarchy; this clustering is divided as Agglomerative clustering and Divisive clustering, wherein agglomerative clustering we start with each element as a cluster and start merging them based upon the features and similarities unless one cluster is formed, this approach is also known as a bottom-up approach. Simultaneously, in divisive clustering, we do vice versa. It is also known to have top-down approachsically unsupervised learning, and choosing the attributes to measure similarity is application-specific.
The Cluster of Data Hierarchy
- Agglomerative Clustering
- Divisive Clustering
Let us take an example of data, marks obtained by 5 students to group them for an upcoming competition.
| Student | Marks |
| A | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Agglomerative Clustering
- To start with, we consider each point/element here weight as clusters and keep on merging the similar points/elements to form a new cluster at the new level until we are left with the single cluster is a bottom-up approach.
- Single linkage and complete linkage are two popular examples of agglomerative clustering. Other than that, Average linkage and Centroid linkage. In a single linkage, we merge in each step the two clusters, whose two closest members have the smallest distance. In complete linkage, we merge in the smallest distance members, which provide the smallest maximum pairwise distance.
- Proximity matrix, It’s the core for performing hierarchical clustering, which gives the distance between each of the points.
- Let us make a proximity matrix for our data given in the table; since we calculate the distance between each of the points with other points, it will be an asymmetric matrix of shape n × n, in our case 5 × 5 matrices.
A popular method for distance calculations are:
- Euclidian distance(Squared)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattan distance
dist((x, y), (a, b)) =|x−c|+|y−d|
Euclidian distance is most commonly used, we will use the same here, and we will go with complex linkage.
| Student(Clusters) | A | B | C | D | E |
| A | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonal elements of the proximity matrix will always be 0. The distance between the point with the same point will always be 0; hence diagonal elements are exempted from grouping consideration.
Here, in iteration 1, the smallest distance is 3; hence we merge A and B to form a cluster, again form a new proximity matrix with cluster (A, B) by taking (A, B) cluster point as 10, i.e. a maximum of (7,10) so newly formed proximity matrix would be
4.5 (9,720 ratings)
View Course
| Clusters | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
In iteration 2, 7 is the minimum distance; hence we merge C and E forming a new cluster (C, E); we repeat the process followed in iteration 1 until we end up with the single cluster, here we stop at iteration 4.
The whole process is depicted in the below figure:
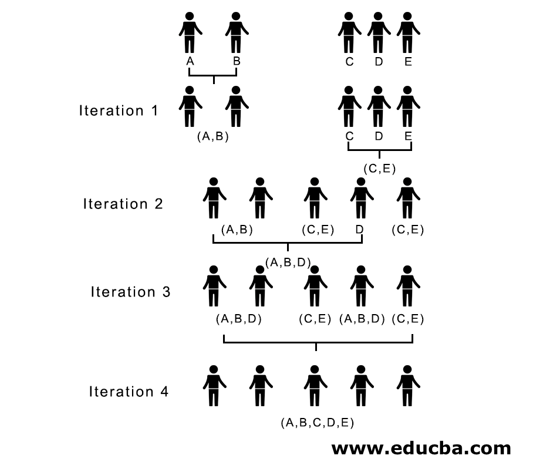
(A,B,D) and (D, E) are the 2 clusters formed at iteration 3; at the last iteration, we can see we are left with a single cluster.
2. Divisive Clustering
First, we consider all points as a single cluster and separate them by the farthest distance until we end off with individual points as individual clusters (not necessarily we can stop in the middle, depends on the minimum number of elements we want in each cluster) at each step. It’s just the opposite of agglomerative clustering, and it is a top-down approach. Divisive clustering is a way repetitive k means clustering.
Choosing between Agglomerative and Divisive Clustering is again application dependent, yet a few points to be considered are:
- Divisive is more complex than agglomerative clustering.
- Divisive clustering is more efficient if we do not generate a complete hierarchy down to individual data points.
- Agglomerative clustering decides by considering the local patterns without considering global patterns initially, which cannot be reversed.
Visualization of Hierarchical Clustering
A Super helpful method to visualize hierarchical clustering, which helps in business, is Dendogram. Dendograms are tree-like structures that record the sequence of merges and splits. The vertical line represents the distance between the clusters; the distance between vertical lines and the distance between the clusters is directly proportional, i.e. more the distance more the clusters are likely to be dissimilar.
We can use the dendogram to decide the number of clusters; draw a line that intersects with the longest vertical line on the dendogram. Several vertical lines intersected will be the number of clusters to be considered.
Below is the example Dendogram.
There are pretty simple and direct python packages and functions to perform hierarchical clustering and plot dendograms.
- The hierarchy from scipy.
- Cluster.hierarchy.dendogram for visualization.
Common Scenarios in which Hierarchical Clustering is used
- Customer Segmentation to product or service marketing.
- City planning to identify the places to build structures/services/building.
- Social Network Analysis, For example, identify all MS Dhoni fans to advertise his biopic.
Advantages of Hierarchical Clustering
The advantages are given below:
- In partial clustering like k-means, the number of clusters should be known before clustering, which is impossible in practical applications. In contrast, in hierarchical clustering, no prior knowledge of the number of clusters is required.
- Hierarchical clustering outputs a hierarchy, i.e. a structure more informative than the unstructured set of the flat clusters returned by partial clustering.
- Hierarchical clustering is easy to implement.
- Brings out results in most of the scenarios.
Conclusion
Type of clustering makes a big difference when data is being presented; hierarchical clustering being more informative and easy to analyze more preferred than partial clustering. And it is often associated with heat maps. Not to forget, attributes chosen to calculate similarity or dissimilarity predominantly influences both clusters and hierarchy.
Recommended Articles
This is a guide to Hierarchical Clustering. Here we discuss the introduction, advantages of Hierarchical Clustering, and Common Scenarios in which Hierarchical Clustering is used. You can also go through our other suggested articles to learn more–
