Updated February 28, 2023

Introduction to Graph Representation

A graph is defined as a data structure with a finite set of nodes, also called vertices and edges. They are represented as an ordered pair in the form of G(V, E) where V(u,v) and E(u,v). The pair in V tells us that there are two vertices and pair in E tells us that there is an edge between u, v nodes of the graph. The edges also might have the cost of moving from vertex u, to v. Graphs are used to depict many real-life problems symbolically and help us visualize the problem’s solution by designing the appropriate algorithm. These are known to be mathematical structures. They are supposed to represent paired relationships among objects. A graph shows the flow of structures between entities.

Graph Components

Below are the two components:

Root Node: We can say it as the starting point or ancestor of all the nodes in a graph. There are no ancestors to the root node. There is exactly one node which is called the root node. In general, the graph traversal starts from this root node.
Leaf Nodes: In a graph, having the number of nodes, we will find some nodes exist at the end level. They are called leaf nodes. They can have n number of incoming edges while no outgoing edges, and that they contain no successors. They only contain ancestor nodes.

Types of Graphs

A graph is made up of vertices or nodes and edges. Thus let us understand types of nodes or vertices in a graph. Now let us explore the types of graphs.

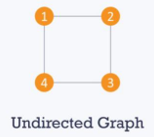
1. Undirected: We can say the undirected graph is a type of graph that has all the edges in a bi-directional fashion which means that edges point freely and they are not having any specific point of direction. The example of an undirected graph is as follows:

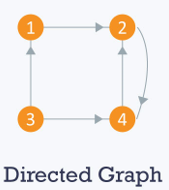
2. Directed: The directed graph can be defined as the graph in which the edges connecting the nodes point in a specific direction, i.e. they are unidirectional. The example is as follows:

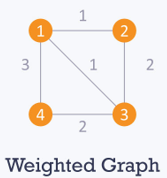
3. Weighted: A weighted graph is when each edge has a cost or weight assigned. Let us consider a graph example for the weighted graph.

4. Cyclic: A graph is said to be cyclic only if the graph consists of a cyclic path. The cyclic path is the path that begins at one end of the vertex or node and ends in the same node. We should also note the graphs that have no cycle are known to be as an acyclic graph.

5. Tree: We can define a tree graph as a graph that is an undirected graph. The tree graph is the one in which there is only one path between two vertices or nodes. A tree is also called an acyclic graph as it has no cycles and contains n-1 edges where n is said to be the number of edges. One of the important properties is that each node in a graph may have more than one root or parent node, which is an interesting differentiation between trees from other graphs. While the point to be noted is that the main parent or root node has no parent or ancestor.

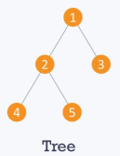
Graph Representation

One can represent a graph in several ways. We have to traverse the graph in computer science using mathematical notations to represent data in the network or other applications. There are two most generic ways of representing a graph in computer science, and we will discuss them as:

1. Adjacency Matrix

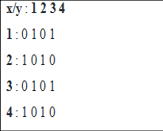
We can define an adjacency matrix as a binary matrix A of V*V elements. The element A x,y is 1 if there exists an edge among vertex i and j or else it is 0. We know that a binary matrix is the one that is either 0 or 1 as its values. In case of an undirected graph we if Ax,y = 1, then Ay,x = 1. In a directed graph, if Ax,y = 1, then Ay,x may or may not be 1. Adjacency matrix gives us constant time and all-time access to running time (O(1) ) that helps to find out if any edge exists between two given nodes. The space complexity is given by O(V2).

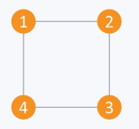
Example: The adjacency matrix of the following undirected graph is:

Ax,y=

The adjacency matrix of the following directed graph is given by:

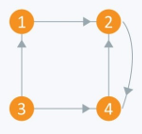
Ax,y=

2. Adjacency List

We can define an adjacency list as an array A composed of separate lists. The array elements represented as Axis a list containing all vertices adjacent to vertex x. In a weighted graph, the edge’s cost is also stored along with the information related to the vertex in the list using the pairs of edges and vertices. In an undirected graph, if vertex y is in list Ax, then vertex x will be in list Ay, and the space complexity is O(V + E).

E.g. of an undirected graph and the adjacency list of the graph is expressed as follows:

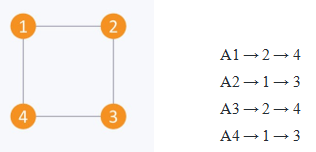
E.g. of a directed graph and the adjacency list of the graph is expressed as follows:

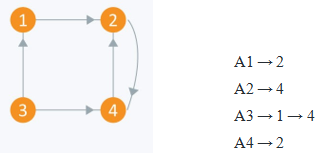
Applications of Graph Representation

The applications of a graph are found to exist in various fields as:

Computer Science: It contains vast applications in Graph Theory, especially making it a specialized computer science field. We also see various networking applications and the basics for the implementation and routing of data on the networks.
Physics and Chemistry: Used to represent the data sets, circuits, chemical formulas, etc.
Biology: For representing the cell and its branches etc.
Social science
Mathematics

Conclusion

Graphs are known to be used in various fields since the beginning of the computing era. They have real-life applications, especially in computer science, for solving problems like networking, the routing problem, circuit networking, etc. E.g. Facebook uses graphs to represent the users as nodes for social networking. The special care is taken to maintain the records at each node in the form of a tree graph.