Updated July 27, 2023
Effect Size Formula (Table of Contents)
What is Effect Size Formula?
The term “effect size” refers to the statistical concept that helps in determining the relationship between two variables from different data groups.
In other words, the concept of effect size can be seen as the measurement of the correlation between the two groups, the standardized mean difference in our case. The formula for effect size is quite simple, and it can be derived for two populations by computing the difference between the means of the two populations and dividing the mean difference by the standard deviation based on either or both the populations. Mathematically, the formula for Effect Size represented as,
where,
- μ1 = Mean of 1st population
- μ2 = Mean of 2nd population
- σ = Standard Deviation
Examples of Effect Size Formula (With Excel Template)
Let’s take an example to understand the calculation of the Effect Size in a better manner.
Effect Size Formula – Example #1
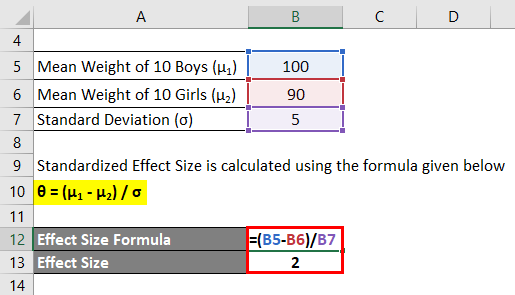
Let us take the example of a picnic group consisting of 10 boys and 10 girls. The mean weight of the 10 boys is 100 lbs, while the mean weight of the 10 girls is 90 lbs. Calculate the standardized effect size across the two groups if the standard deviation is 5 lbs.
Solution:
Standardized Effect Size is calculated using the formula given below
θ = (μ1 – μ2) / σ
- θ= (100 lbs – 90 lbs) / 5 lbs
- θ= 2
Therefore, the standardized effect size of weight across the two groups is 2.
Effect Size Formula – Example #2
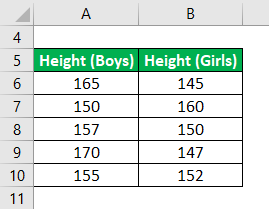
Let us take the example of a class of 10 students (5 boys and 5 girls). There was a medical check-up day at the school. The height was measured as part of the check-up. Calculate the standardized effect size across the two groups based on the given information.
Solution:
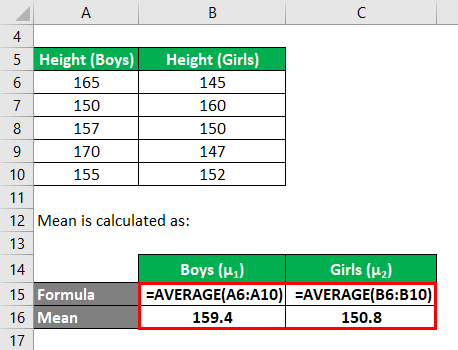
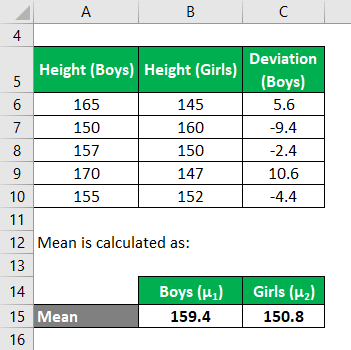
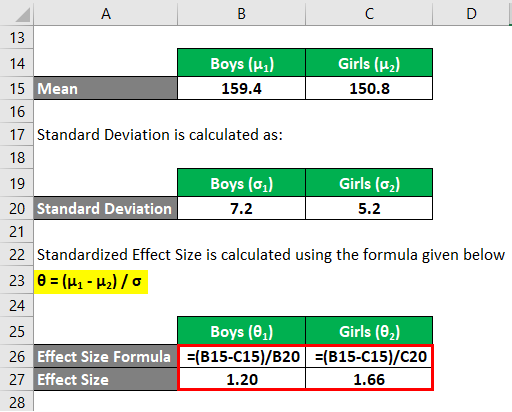
Mean is calculated as:
- Mean Height of 5 boys (μ1) = 159.4 cm
- Mean Height of 5 girls, (μ2) = 150.8 cm
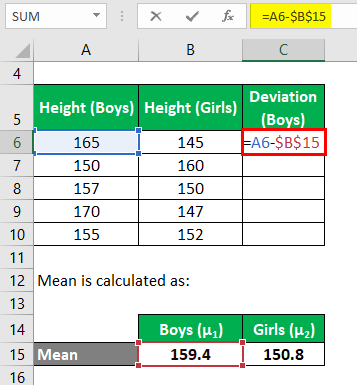
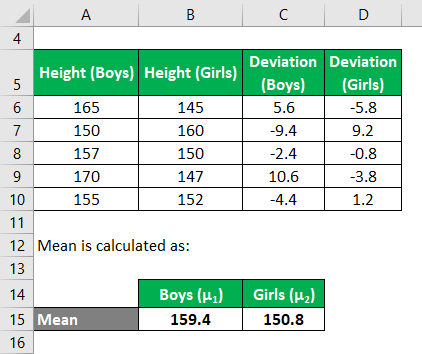
Now, we need to calculate the deviations based on a group of boys,
Similarly, calculate for all the group of boys.
Similarly, calculate all the deviations based on a group of girls,
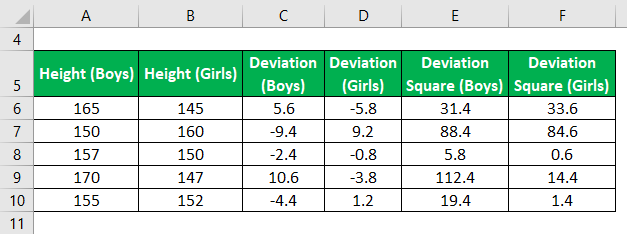
Calculate the square of the deviations for both the group.
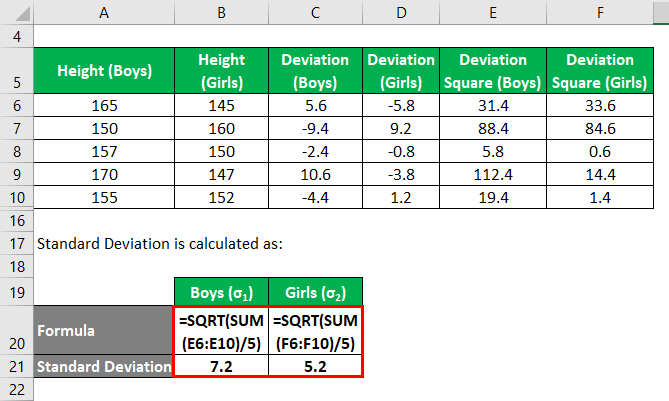
Standard Deviation is calculated as:
- Standard Deviation (σ1) = 7.2 cm
- Standard Deviation (σ2) = 5.2 cm
Standardized Effect Size is calculated using the formula given below
θ = (μ1 – μ2) / σ
- Boys (θ1) = (159.4 cm – 150.8 cm) / 7.2 cm
- Boys (θ1) = 1.20
- Girls (θ2) = (159.4 cm – 150.8 cm) / 5.2 cm
- Girls (θ2) = 1.66
Therefore, the standardized effect size of height across the groups of boys and girls is 1.20 based on standard deviation based on a group of boys, while it is 1.66 using a group of girls.
Explanation
The formula for effect size can be derived by using the following steps:
Step 1: Firstly, determine the mean of the 1st population by adding up all the available variable in the data set and divide by the number of variables. It is denoted by μ1.
Step 2: Next, determine the mean for the 2nd population in the same way as mentioned in step 1. It is denoted by μ2.
Step 3: Next, calculate the mean difference by deducting the mean of the 2nd population (μ2 in step 2) from that of the 1st one (μ1 in step 1), as shown below.
Mean Difference = μ1 – μ2
Step 4: Next, determine the standard deviation either based on any of the populations of both. It is denoted by σ.
Step 5: Finally, the formula for effect size can be derived by dividing the mean difference (step 3) by the standard deviation (step 4), as shown below.
θ = (μ1 – μ2) / σ
Relevance and Uses of Effect Size Formula
It is very important to understand the concept of effect size because it is a statistical tool that helps in quantifying the size of the difference between two groups, which can be considered to be the true measure of the significance of the difference. In other words, it is a statistical method to measure the relationship between two variables from a different group of data sets. Now, effect size enables readers to grasp the magnitude of the mean differences between two groups, while statistical significance validates that the findings are not due to chance. So, both effect size and statistical significance are essential for a comprehensive understanding of the statistical experiment. As such, it is advisable to present the effect size and the statistical significance, along with the confidence interval, as both the metric complement each other and enables better understanding.
Effect Size Formula Calculator
You can use the following Effect Size Calculator
| µ1 | |
| µ2 | |
| σ | |
| θ | |
| θ = |
|
|
Recommended Articles
This has been a guide to Effect Size Formula. Here we discuss How to Calculate Effect Size along with practical examples. We also provide an Effect Size Calculator with a downloadable excel template. You may also look at the following articles to learn more –