Confidence Interval Formula

Confidence Interval Formula (Table of Contents)

• Formula
• Examples
• Calculator

What is the Confidence Interval Formula?

In statistics, the term “Confidence Interval” refers to the range of values within which the true population value would lie in the case of a sample out of the population. In other words, the confidence interval represents the amount of uncertainty expected while determining the sample population estimate or mean of a true population. The use of confidence intervals makes the estimation of the sample population estimate more manageable.

The formula for confidence interval can be calculated by subtracting and adding the margin of error from and to the sample mean. The margin of error is computed on the basis of the given confidence level, population standard deviation, and the number of observations in the sample. Mathematically, the formula for the confidence interval is represented as,

OR

Where,

• x̄: Sample Mean
• z: Confidence Coefficient
• ơ: Population Standard Deviation
• n: Sample Size

Example of Confidence Interval Formula (With Excel Template)

Let’s take an example to understand the calculation of the Confidence Interval Formula in a better manner.

Confidence Interval Formula – Example #1

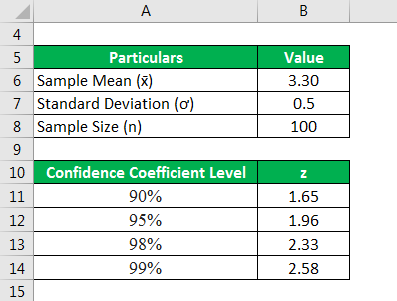
Let us take the example of 100 respondents who were surveyed for their feedback on customer service. The survey was on a scale of 1 to 5 with 5 being the best, and it was found that the average feedback of the respondents was 3.3 with a population standard deviation of 0.5. Determine the confidence interval for –

• 90% Confidence Level
• 95% Confidence Level
• 98% Confidence Level
• 99% Confidence Level

Solution:

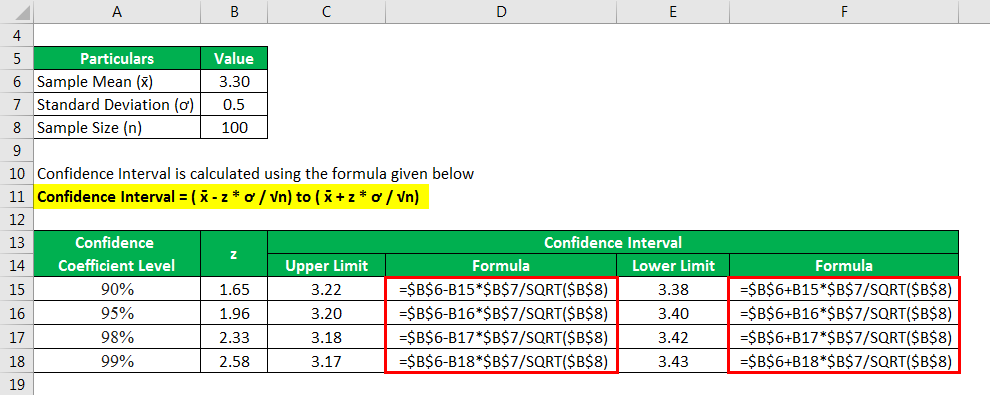
Confidence Interval is calculated using the formula given below

Confidence Interval = ( x̄ – z * ơ / √n) to ( x̄ + z * ơ / √n)

Overall Calculation for the Upper Limit and Lower Limit as below

For 90%

• Confidence Interval = (3.30 – 1.645 * 0.5 / √100) to (3.30 + 1.645 * 0.5 / √100)
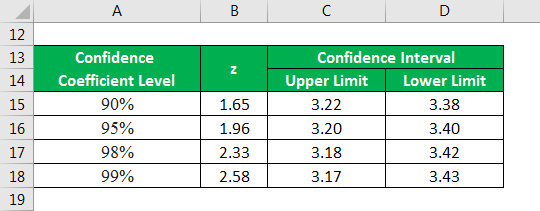
• Confidence Interval = 3.22 to 3.38

Therefore, the Confidence Interval at a 90% confidence level is 3.22 to 3.38.

For 95%

• Confidence Interval = (3.30 – 1.96 * 0.5 / √100) to (3.30 + 1.96 * 0.5 / √100)
• Confidence Interval = 3.20 to 3.40

Therefore, the Confidence Interval at a 95% confidence level is 3.20 to 3.40.

For 98%

• Confidence Interval = (3.30 – 2.33 * 0.5 / √100) to (3.30 + 2.33 * 0.5 / √100)
• Confidence Interval = 3.18 to 3.42

Therefore, the confidence interval at 98% confidence level is 3.18 to 3.42.

For 99%

• Confidence Interval = (3.30 – 2.58 * 0.5 / √100) to (3.30 + 2.58 * 0.5 / √100)
• Confidence Interval = 3.17 to 3.43

Therefore, the confidence interval at 99% confidence level is 3.17 to 3.43.

From the above illustration, it can be seen that the confidence interval of a sample spreads out with the increase in confidence level.

Explanation

The formula for Confidence Interval can be calculated by using the following steps:

Step 1: Firstly, determine the sample mean based on the sample observations from the population data set. It is denoted by.

Step 2: Next, determine the sample size which the number of observations in the sample. It is denoted by n.

Step 3: Next, determine the population standard deviation on the basis of sample observations, mean and sample size. It is denoted by ơ.

Step 4: Next, determine the confidence coefficient or z-score on the basis of the desired confidence level.

Step 5: Next, compute the margin of error by using sample size (step 2), population standard deviation (step 3) and confidence coefficient (step 4).

Margin of Error = z * ơ / √n

Step 6: Finally, the formula for confidence interval can be calculated by subtracting and adding the margin of error (step 5) from and to sample mean (step 1) as shown below:

Confidence Interval = ( x̄ – z * ơ / √n) to ( x̄ + z * ơ / √n)

OR

Confidence Interval = x̄ ± z * ơ / √n

Confidence Interval Formula Calculator

You can use the following Confidence Interval Formula Calculator

Relevance and Use of Confidence Interval Formula

It is important to understand the concept of the confidence interval as it indicates the precision of a sampling method. Basically, it indicates how stable is the sample population estimate such that there will be a minimum deviation from the original estimate in case the sampling is repeated again and again. There is some confusion about what exactly is confidence interval and confidence level. Please note that a 95% confidence level doesn’t mean that there is a 95% chance that the population parameter will fall within the given interval. The 95% confidence level means that the estimation procedure or sampling method is 95% reliable.

Recommended Articles

This is a guide to the Confidence Interval Formula. Here we discuss how to calculate the Confidence Interval Formula along with practical examples. We also provide a Confidence Interval a downloadable excel template. You may also look at the following articles to learn more –

1. How to Calculate Indexation?
2. Example of Effect Size Formula
3. Calculation of Annuity Formula
4. What is Quartile?