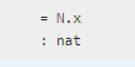Updated July 4, 2023
Introduction to Coq Language
Coq Language is a functional programming language and is dependently typed, which is used to write programs and verify that user specifications are met accordingly. This type of functional programming language is focused on simple and mathematical intuition. Coq implements a dependently typed functional programming language when viewed as a programming language. And when viewed as a logical system, Coq implements a higher-order theory.
Why do we Need a Coq Language?
- The development of Coq has been supported since 1984, initiated its development by Gerard Huet and Thierry Coquand; more than 40 people have contributed interesting features to the core system.
- Coq is mainly implemented with C, and a plug-in mechanism can extend the core system.
- Coq is dependently typed; this methodology helps develop the software perfectly while code construction and possible bugs and exceptions are ruled out.
- As a functional language, this Coq language’s common features include algebraic data types and pattern matching.
- It also gives ease of coding and manipulates rich data structures.
- Coq programming also offers polymorphic type structures supporting code abstraction and reuse.
- Coq also provides a specification language known as Gallina.
- Programs written in Gallina have weak normalization property, which is a distinct property that implies programs always terminate.
- This particular feature is distinct since infinite loops are too common in other programming language (Non-Terminating programs).
Working of Coq Language or its Usage
Coq language is designed for developing mathematical proofs and writing formal specifications. It verifies whether the programs are correct or not concerning the specifications. Gallina, the specification language, represents the programs, properties, and proofs for the Coq language.
Coq language has the Curry – Harvard Isomorphism technique. Using this, programs, properties, and proofs are formalized into a language called Calculus of Inductive Constructions, an Alpha–Calculus with a rich type system.
In Coq, all logical judgments are typing judgments. The heart of the Coq language is a type-checking algorithm, which checks the correctness of proofs. In other words, the Type checking algorithm checks if the program compiles to the specifications. Coq provides interactive proof assistance to build proofs using specific programs called tactics. All these services of Coq proof assistant are accessible by command language interpretation called Vernacular, as Coq has an interactive mode where commands are interpreted as user types.
There are two types of modes where commands are processed from a file:
- Interactive Mode: Users quickly develop theories and proofs and query the system for available theorems and definitions. The Coq Integrated Development Environment (IDE) is commonly used to run and interact with this interactive mode.
- Compiled Mode: This mode acts as a proof checker, which takes a complete development file to ensure correctness. Coq’s compiler provides an output file containing a similar input representation. This mode runs with coqc command.
Advantages and Disadvantages of Coq Language
Given below are the advantages and disadvantages mentioned:
Advantages:
- Coq lacks many reasoning principles, which are common in mathematical practices.
- The designers designed the Coq language to allow people to add reasoning principles safely as extra axioms.
- They built logic from the ground or scratch.
- Coq has many powerful automation procedures, such as congruence and omega, but these are not generally applicable and require more explicit proofs.
Disadvantages:
- This becomes a problem in proving simple theorems but makes an issue when the proof automation is not that powerful.
- Coq has tactic language for writing the proofs, known as Ltac. A different situation arises in supporting user-defined and proof automation procedures.
- Ltac has some design problems but allows users to encode fairly complicated proof automation procedures in a lightweight manner.
- Coq will also allow users to write plugins in Coq’s implementation language for some heavier tasks.
- There is only a single higher-level automation language, i.e., Ltac, and plugins are the only way to customize these programs.
- Coq is more strict, using intuitionistic logic. It has several orders and allows type dependencies that are non-terminating in some of circumstances.
Coq Objects Sorted into Two Categories
- Prop sort
- Type sort
1. Prop sort is for propositions. We can define new predicates by using inductive reasoning or abstracting existing propositions.
Typical propositions:
∀ A B : Prop, A /\ B -> B \/ B
∀ x y : Z, x * y = 0 -> x = 0 \/ y = 0
New predicated defined inductively:
Inductive even : N -> Prop :=
| even_0 : even 0
| even_S n : odd n -> even (n + 1)
with odd : N -> Prop :=
| odd_S n : even n -> odd (n + 1).
Abstracting existing propositions:
Definition divide (x y:N) := ∃ z, x * z = y.
Definition prime x := ∀ y, divide y x -> y = 1 \/ y = x.
2. Type sort is for well-formed mathematical structures and data types.
Basic Coq example:
Z -> Z * Z
Inductive structure:
Inductive nat : Set :=
| 0 : nat
| S : nat -> nat.
Inductive list (A:Type) : Type :=
| nil : list A
| cons : A -> list A -> list A.
Types of tuples:
Structure monoid := {
dom : Type ;
op : dom -> dom -> dom where "x * y" := (op x y);
id : dom where "1" := id;
assoc : ∀ x y z, x * (y * z) = (x * y) * z ;
left_neutral : ∀ x, 1 * x = x ;
right_neutral : ∀ x, x * 1 = x
}.Examples of Coq Language
Given below are the examples:
Example #1
Simple module interactively.
Code:
Module M.
Definition T := nat.
Definition x := 0.
Definition y : bool.Output:
Example #2
Definition of using N module type expression.
Code:
Module Type SIG'.
Definition T : Set := nat.
Parameter x : T.
End SIG'.
Module N : SIG' := M.
Module P <: SIG := M.
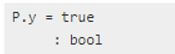
Print P.y.Output:
Example #3
Functor creator.
Code:
Module Two (X Y: SIG).
Definition T := (X.T * Y.T)%type.
Definition x := (X.x, Y.x).
End Two
Module Q := Two M N.
Eval compute in (fst Q.x + snd Q.x).Output:
Career in Coq Language
- Operating engineers have many career opportunities available to them in various countries.
- People with a passion for functional programming and an interest in mathematics and proof assistants( Coq ) can have people surrounded by like-minded individuals.
- Most candidates recruited in this technology should have a Degree in Mathematics or Computing and a Secondary Degree in MPhil.
- Have experience in functional programming, with design knowledge in simple and elegant solutions.
- Also should have experience in delivering enterprise-quality software.
Conclusion
We have seen what Coq language is and how it works. We have also seen some advantages and disadvantages, their uses, and how the Coq language works. There are also career openings for this Coq language who have experience in proofs programming. We have also seen some of examples with Coq IDE.
Recommended Articles
We hope that this EDUCBA information on “Coq Language” was beneficial to you. You can view EDUCBA’s recommended articles for more information.