Updated April 1, 2023
Introduction to Binary Search Tree Insertion
The following article provide an outline for Binary search tree insertion. A binary search tree is a Binary tree with some additional conditions. Let’s understand the first binary tree, Binary tree is a data structure in which each Node has a maximum of two children or each node connected to at most two subtrees.
Binary Search Tree is a special case of binary tree in which left child value should be less than to parent node and the value of right child of parent node should be greater than the parent node. Where the parent node is the current node and the left and right child are nodes of which the address stored in the current node of the Binary Search Tree.
Insertion is one of the operations of a Binary search tree in which a new value is inserted at any leaf node keeping in mind that the properties of the binary search tree sustain.
Syntax: –
Let’s understand the structure of Node in the Binary Search Tree. In Binary Search Tree Node there are three components.
- Value – Value store at Node
- *Left – Address of Left Child Node
- *Right – Address of Left-Right Node
How to perform Binary Search Tree Insertion?
As in a binary search tree, all values in the left subtree are always less than the node value and all values of the right subtree are always greater than the node value. So, in Inorder traversal on Binary Search Tree gives a sorted list of values.
The main operations in Binary Search Tree are: -: –
- Find any value in Binary Search Tree.
- Find the Maximum value in Binary Search Tree. In a binary search tree, the rightmost leaf node value is always maximum.
- Find the minimum value in Binary Search Tree. In a binary search tree left most leaf node value is always minimum.
- Insertion in Binary Tree: –
We perform an insertion operation to insert any value in the binary search tree. In a binary search tree, any value always inserts at the leaf node and should follow the properties of the binary search tree. To insert the value, first check the node, if the node is NULL or not. If the node is NULL, then we update the node value to insert the value. In simple words, we have to find the leaf node in which the value-inserting node will be a child.
If a node is not NULL, then we compare the inserting value with the value of a node. If the value of a node will be greater than the inserting value, then we move to the left child of that node and do the same check node is NULL or not.
If the value of a node is smaller than the inserting value, then we move to the right child of that node. Now Let’s understand this with an example.
The time complexity of the insertion operation in the Binary Search Tree is O(H) where H is the depth of the Binary Search Tree. In the worst-case Depth of the Binary search, the tree is equal to the total nodes in the binary search tree.
Examples of Binary Search Tree Insertion
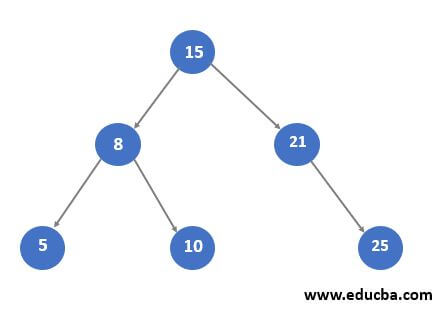
Let’s take the existing Binary Search Tree as shown in this figure, and insert the value 18.
Every node in the Binary Search Tree contains a value with which to compare the inserting value. Create an InsertNode function that takes the pointer of the node and the value to be inserted and returns the updated node.
Step 1. In the given example call the InsertNode function and pass the root Node of the existing Binary Search Tree and the value which is 18. Now in the InsertNode function, as the root is not NULL so next, we compare the inserting value with the root node. As we can see root node has a value is 15 and the inserting value is 18 which is greater. So we call recursively InsertNode and pass the right child of root and the inserting value. It will return the updated right child of the root node.
Step2. Now in this also root node is not NULL so we compare the inserting with a root node. The root node value is 21. Compare with inserting value 18. Now insert a value that is smaller than the root node value. So this time we recursively call InsertNode and pass the left child of the root and the inserting value. It will return the updated left child of the root node.
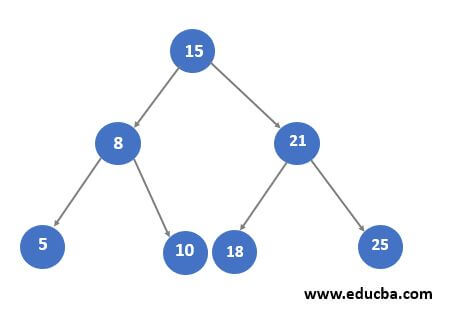
Step 3. Now as we can see in the above figure root node is NULL so we update the value to insert the value and return the updated root node.
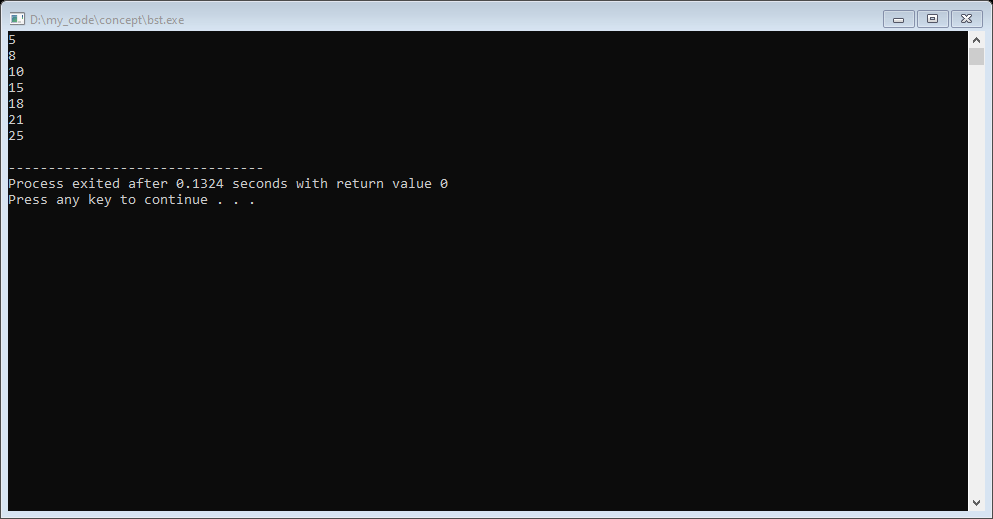
Step 4. So like this all recursive calls will complete and to check the inserting value, we perform Inorder traversal on this Binary Search Tree and It should return all values in sorted order.
Advantages of Binary Search Tree
In Binary Search Tree sorting and Searching operations are very efficient. We can find any value in the Binary Search Tree in O(H) Time Complexity where H is the maximum depth of the Binary Search Tree. Similarly to that we can get the minimum and maximum of trees by getting the value of the leftmost and rightmost leaf nodes.
Implementation:
struct BSTNode {
int value; // element value
struct BSTNode * left; //To store address of left child
struct BSTNode * right; //To store address of right child
};
struct BSTNode *InsertNode(struct BSTNode *root,int data){
if(root == NULL){
root = (struct BSTNode*)malloc(sizeof(struct BSTNode));
root->value=data;
root->left=NULL;
root->right=NULL;
}
else{
if(data<root->value){
root->left=InsertNode(root->left,data);
}
else if(data>root->value){
root->right=InsertNode(root->right,data);
}
}
return root;
}
void displayTreeInorder(struct BSTNode *root){
if(root!=NULL){
displayTreeInorder(root->left);
cout<<root->value<<endl;
displayTreeInorder(root->right);
}
}
int main(){
BSTNode *root=NULL;
root=InsertNode(root,15);
root=InsertNode(root,21);
root=InsertNode(root,8);
root=InsertNode(root,25);
root=InsertNode(root,10);
displayTreeInorder(root);
Output:-
Conclusion
A binary search tree is a solution to get the sorted array using one Inorder traversal. The memory is taken in Binary Search Tree and Binary Tree is the same. A Binary Search Tree is an important concept in the Searching and Sorting algorithm.
Recommended Articles
This is a guide to Binary search tree insertion. Here we discuss How to perform binary search tree insertion along with the examples. You may also have a look at the following articles to learn more –