Updated March 31, 2023
Introduction to B+ tree insertion
The following article provide an outline for B+ tree insertion. B+ trees are used to implement database indexes by implementing dynamic multilevel indexing. In B+ trees, leaf nodes denote the actual data pointers, which is the main drawback in B+ trees. In the B+ tree, all leaf nodes are present at the same height. This process reduces the number of entries into a node of a B+ tree and reduces the search time.
In the B+ tree, the leaf nodes are linked using Linked Lists to support random access and sequential access of the elements. Since it stores the information in linked lists, it occupies more space than B-tress.
Characteristics of B+ trees
- Data points are stored only in leaf nodes.
- Internal nodes contain keys.
- To directly search the elements, we use keys in B+ trees.
- If there are ‘m’ elements, then there will be a maximum of ‘m-1’ keys and at least ‘[m/2] -1’ keys.
- The root node has at least two children and at least one key.
- For ‘m’ elements, each node except the root can have at least ‘m/2’ children and a maximum of ‘m’ children.
Steps for inserting data points in B+ trees
- Every element is to be inserted in the leaf node.
- If an overflow condition occurs in the leaf nodes, follow the below steps:
- Split the leaf into two separate nodes along with the other nodes.
- The first node contains the ceiling value of (m-1)/2.
- The second node contains the remaining nodes from the above nodes.
- Insert the element in the left parent node in the Right-biased tree.
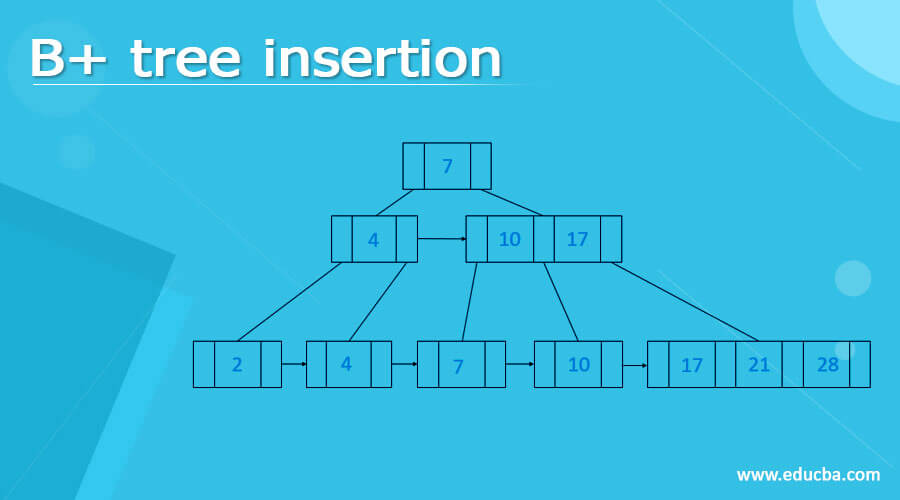
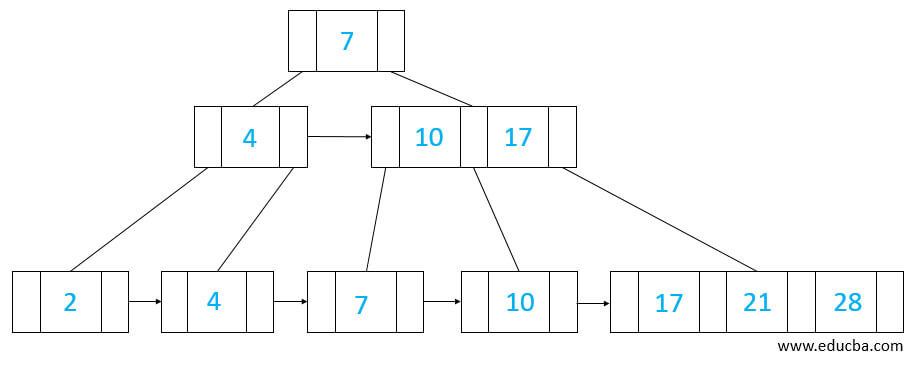
Representation of a B+ tree and inserting a data point
Before moving on to the algorithm, let’s look at the working pattern and properties of this B+ tree.
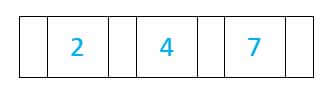
- Let us take an example of seven elements as shown below.
2, 4, 7, 10, 17, 21, 28
- Assume that the order is three, then each node must contain at least three nodes and two keys.
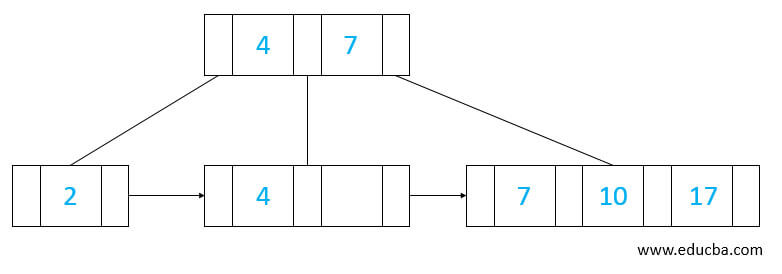
- Since we don’t have space to insert 10, which is an overflow condition in the node with three elements, we will split the middle element and then insert it as shown.
- In the same way, we will insert 17 after 10 in the third node.
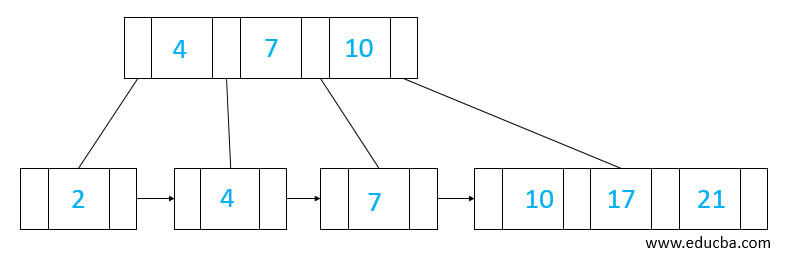
- Since we don’t have space after 17 to insert 21 in the above third node, we will split 10 from the last leaf node to insert 21 by placing 10 after 7 in the root node, as shown.
- To insert 28, we need to send 17 to the above node but, there is no space to insert 17 so, we need to split 7 to place 17 and finally insert 28.
Step 4: If the leaf is full, insert the element and then balance the tree to maintain order.
- In the last step, whatever the data points that we have entered have reached the leaf node.
Algorithm of B+ Tree Insertion
The following is the algorithm to insert an element into the B+ tree.
Step 1: Check if the root node has at least two children.
Step 2: Traverse through the tree to the leaf node.
Step 3: If the leaf is not full, insert the element into the key in increasing order.
Step 5: To balance the tree break the inserted node at the m/2th position
Step 6: Add the m/2th key to the parent node.
Step 7: If the parent node is full, recursively call step 2 and step 3.
Source Code to insert an element into the B+ tree
temp2 = current_node.values
for i in range(len(temp2)):
if (value == temp2[i]):
current_node = current_node.keys[i + 1]
break
elif (value < temp2[i]):
current_node = current_node.keys[i]
break
elif (i + 1 == len(current_node.values)):
current_node = current_node.keys[i + 1]
break
return current_node
# Find the node
def find(self, value, key):
l = self.search(value)
for i, item in enumerate(l.values):
if item == value:
if key in l.keys[i]:
return True
else:
return False
return False
# Inserting at the parent
def insert_in_parent(self, n, value, ndash):
if (self.root == n):
rootNode = Node(n.order)
rootNode.values = [value]
rootNode.keys = [n, ndash]
self.root = rootNode
n.parent = rootNode
ndash.parent = rootNode
return
parentNode = n.parent
temp3 = parentNode.keys
for i in range(len(temp3)):
if (temp3[i] == n):
parentNode.values = parentNode.values[:i] + \
[value] + parentNode.values[i:]
parentNode.keys = parentNode.keys[:i +
1] + [ndash] + parentNode.keys[i + 1:]
if (len(parentNode.keys) > parentNode.order):
parentdash = Node(parentNode.order)
parentdash.parent = parentNode.parent
mid = int(math.ceil(parentNode.order / 2)) - 1
parentdash.values = parentNode.values[mid + 1:]
parentdash.keys = parentNode.keys[mid + 1:]
value_ = parentNode.values[mid]
if (mid == 0):
parentNode.values = parentNode.values[:mid + 1]
else:
parentNode.values = parentNode.values[:mid]
parentNode.keys = parentNode.keys[:mid + 1]
for j in parentNode.keys:
j.parent = parentNode
for j in parentdash.keys:
j.parent = parentdash
self.insert_in_parent(parentNode, value_, parentdash)
# Print the tree
def printTree(tree):
lst = [tree.root]
level = [0]
leaf = None
flag = 0
lev_leaf = 0
node1 = Node(str(level[0]) + str(tree.root.values))
while (len(lst) != 0):
x = lst.pop(0)
lev = level.pop(0)
if (x.check_leaf == False):
for i, item in enumerate(x.keys):
print(item.values)
else:
for i, item in enumerate(x.keys):
print(item.values)
if (flag == 0):
lev_leaf = lev
leaf = x
flag = 1
record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert('5', '33')
bplustree.insert('15', '21')
bplustree.insert('25', '31')
bplustree.insert('35', '41')
bplustree.insert('45', '10')
printTree(bplustree)
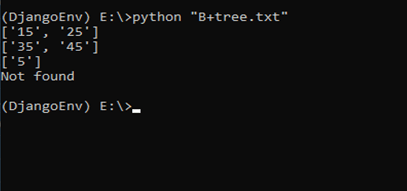
if(bplustree.find('5', '34')):
print("Found")
else:
print("Not found")
Output:
Conclusion
- B+ trees are used to implement database indexes by implementing dynamic multilevel indexing.
- For ‘m’ elements, each node except the root can have at least ‘m/2’ children and a maximum of ‘m’ children.
- In the B+ tree, the leaf nodes are linked using Linked Lists.
Recommended Articles
This is a guide to B+ tree insertion. Here we discuss the Representation of a B+ tree and inserting a data point along with the algorithm. You may also have a look at the following articles to learn more –