Updated March 8, 2023
Definition of AVL Tree
AVL tree is also known as self-balancing binary search tree (BST) because each node in this tree has extra information about the node or the position of the node known as the balance factor. The balance factor contains -1, 0 or +1.
Deletion Operation in AVL Tree
When we delete an element in the AVL tree, this disturbs the balance factor of the whole tree for which the tree needs to be balanced again. To rebalance it, rotations are performed on it namely Left Rotation and Right rotation.
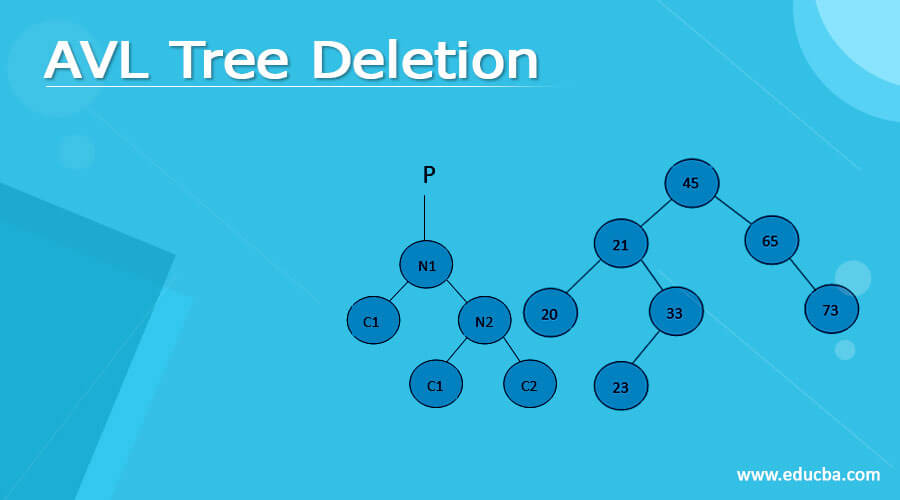
Left Rotation
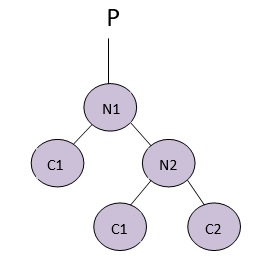
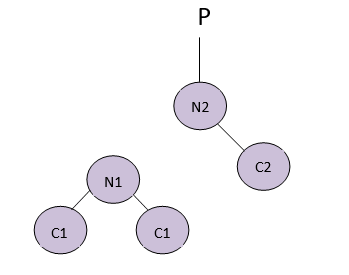
1. Let’s assume the below AVL tree for left rotation.
2. If N2 has a left subtree, then assign N1 as the parent of the left subtree of N2.
• If N1 doesn’t have a parent, make N2 the parent of N1, which is the root of the tree.
• If N1 is the left child of any parent, then make N2 the left child of that parent.
• If the above two conditions don’t work, then make N2 the right child of the parent.
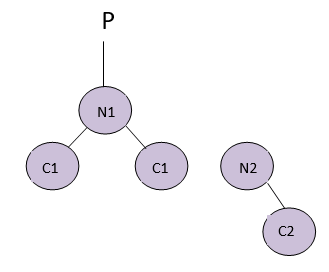
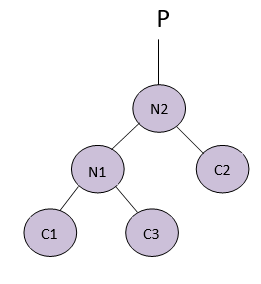
This is the final balanced tree when we perform Left rotation on it. Right rotation is also done similarly to the AVL tree.

Algorithm to delete an element in AVL tree
A node should always be deleted as a leaf node. When a node is deleted the balance factors of the tree get disturbed and there is a need to rebalance the tree to get the correct balance factors.
1. Find the node to be deleted using a recursion algorithm.
2. There are three conditions to delete a node
• If the node which is to be deleted is a leaf node, then that node is removed directly.
• If the node contains one child then swap them and then delete the leaf node which contains the key element.
• If the node contains two children, then find the inorder successor of that node which is to be deleted, that is, the value which is less than the key will be at the right subtree.
1. Substitute the node which is to be deleted with the before node.
2. Remove the substituted leaf node.
3. Balance the tree using any suitable rotation techniques.
Source Code
# AVL tree implementation in Python
import sys
# Create a tree node
class TreeNode(object):
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
# Function to insert a node
def insert_node(self, root, key):
# Find the correct location and insert the node
if not root:
return TreeNode(key)
elif key < root.key:
root.left = self.insert_node(root.left, key)
else:
root.right = self.insert_node(root.right, key)
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
# Update the balance factor and balance the tree
balanceFactor = self.getBalance(root)
if balanceFactor > 1:
if key < root.left.key:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if key > root.right.key:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
# Function to delete a node
def delete_node(self, root, key):
# Find the node to be deleted and remove it
if not root:
return root
elif key < root.key:
root.left = self.delete_node(root.left, key)
elif key > root.key:
root.right = self.delete_node(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = self.getMinValueNode(root.right)
root.key = temp.key
root.right = self.delete_node(root.right,
temp.key)
if root is None:
return root
# Update the balance factor of nodes
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
balanceFactor = self.getBalance(root)
# Balance the tree
if balanceFactor > 1:
if self.getBalance(root.left) >= 0:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if self.getBalance(root.right) <= 0:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
# Function to perform left rotation
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Function to perform right rotation
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Get the height of the node
def getHeight(self, root):
if not root:
return 0
return root.height
# Get balance factore of the node
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def getMinValueNode(self, root):
if root is None or root.left is None:
return root
return self.getMinValueNode(root.left)
def preOrder(self, root):
if not root:
return
print("{0} ".format(root.key), end="")
self.preOrder(root.left)
self.preOrder(root.right)
# Print the tree
def printHelper(self, currPtr, indent, last):
if currPtr != None:
sys.stdout.write(indent)
if last:
sys.stdout.write("R----")
indent += " "
else:
sys.stdout.write("L----")
indent += "| "
print(currPtr.key)
self.printHelper(currPtr.left, indent, False)
self.printHelper(currPtr.right, indent, True)
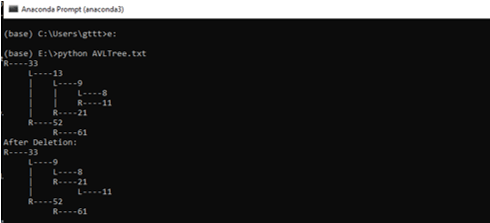
myTree = AVLTree()
root = None
nums = [33, 13, 52, 9, 21, 61, 8, 11]
for num in nums:
root = myTree.insert_node(root, num)
myTree.printHelper(root, "", True)
key = 13
root = myTree.delete_node(root, key)
print("After Deletion: ")
myTree.printHelper(root, "", True)
Output:
Time Complexity of Deletion in AVL tree
The time complexity of the AVL tree will be the same as Binary Search Tree. Getting the balance factor by performing various rotating operations and updating the height of the balance tree takes constant time. So, the time complexity will be similar to the time complexity of the Binary search tree which is O(h), where h is the height of the tree. Since the height of the AVL tree is log, the time complexity of Deleting an element in the AVL tree will be O(logn).
Conclusion
- AVL tree is also known as self-balancing binary search tree(BST) because each node in this tree has extra information about the node or the position of the node known as the balance factor.
- We delete an element only in the leaf node in an AVL tree, if the key is not present in the leaf node we perform in order operations to bring it to the leaf node, then we delete the element.
- When we delete an element in the AVL tree, this disturbs the balance factor of the whole tree for which the tree needs to be balanced again.
- The time complexity of the Deletion operation of an AVL tree is O(logn)
Recommended Articles
This is a guide to AVL Tree Deletion. Here we discuss the definition, Deletion Operation in AVL Tree, Algorithm to delete an element in the AVL tree. You may also have a look at the following articles to learn more –