Updated December 6, 2023

Introduction of Array Implementation of Queue

Implementing a queue using an array has proved to be one of the most accessible and straightforward strategies for saving time and memory. Due to its contiguous nature, enqueue and dequeue operations are fast and predictable. It is capable of handling applications with established capacity. The array-based queue is an organized way of administrating and processing elements in a systematic and reachable format, and it can be easily aligned with multiple scenarios with minor overhead.

Introduction
What is a Queue?
Basic Operations on Queue
Algorithm for the Implementation of Queue Using Array
How to Implement Queue Using Array?
Time Complexity
Examples
Applications of Queue
Advantages and Disadvantages

Key Takeaways

Contiguous memory – Adjacent memory location without any storage voids.
Lightweight – Doesn’t require any help from third-party libraries.
Basic operations take almost the same time to perform and hence improve predictability.
Comfortable with first-come, first-serve applications.
Capable of controlling data management between different areas of an application.
Expert in administrating processes lined up for operation.

What is a Queue?

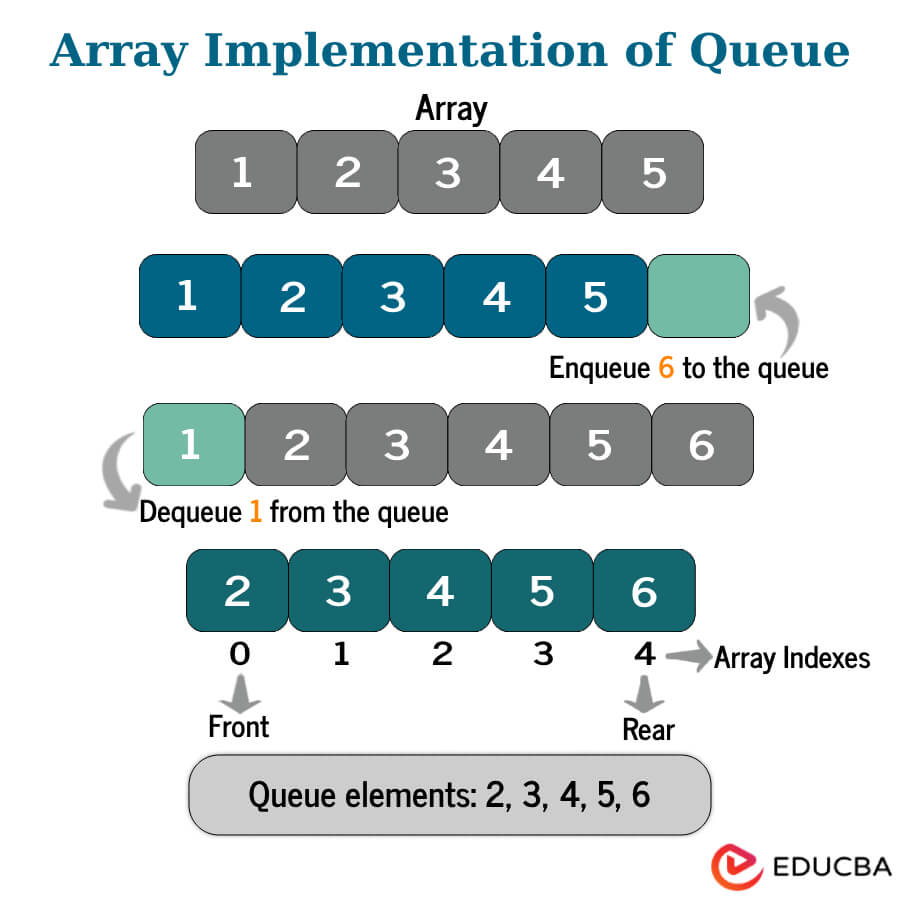
A queue is a data structure that works according to the FIFO (First In, First Out) principle. This means that the first item to enter the queue will be the first one to be eliminated. Items or elements are added to the queue from the rear end, and this addition is called enqueue. The items are removed from the front end, known as dequeue.

There are two types of queues.

Linear queue: The simplest example of a linear queue is people standing in line to buy a movie ticket. People join the queue from the end, and people leave the queue from the front.
Circular queue: This optimized version of a linear queue joins the front and rear ends to maximize performance and avoid memory wastage. Unlike in a linear queue, adding and eliminating elements can be done from any position.

Basic Operations on Queue

Some fundamental operations on a queue include performing the following actions:

Enqueue(): The most basic operation of addition of an element to the queue from the rear end (in case of linear queue) and from any position (in case of circular queue).
Dequeue(): Elimination of an element from the queue from the front end (in case of linear queue) and any position (in case of circular queue).
Peek(): Grabbing the data element from the queue’s front side without eliminating the aspect.
isFull(): An operation to determine whether the queue is full. It returns a boolean value.
isEmpty(): An operation to determine whether the queue is empty. It returns a boolean value.

Algorithm for the Implementation of Queue Using Array

Step1: Initialization

array_size = n
rear = -1
front = -1

Step2: Enqueue process

if(rear == array_size-1) // checking isFull condition
display overflow message
else
increment the value of the rear from -1 to 0.
at queue[rear] = input_value

Step3: Dequeue Process

Note - after incrementing, the front now points to 0 from -1
if(front == -1) // checking isEmpty condition.
display empty queue msg.
else
eliminate the element from queue[0]

Step 4: Repeat the process

Step 5: After deleting all the elements from the list, the front value surpasses the rear value, and the queue becomes empty. So, the rear and front automatically reset to -1 at the initialization stage (step 1).

How to Implement Queue Using Array?

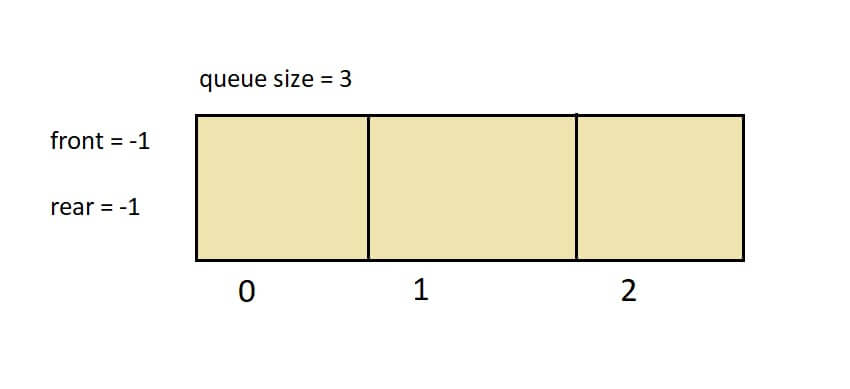
1. Initialize the queue size, front and rear.

queue_size = 3

rear = -1

front = -1

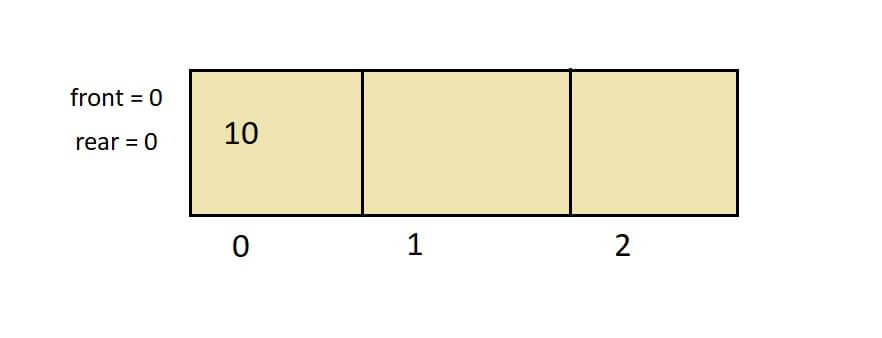
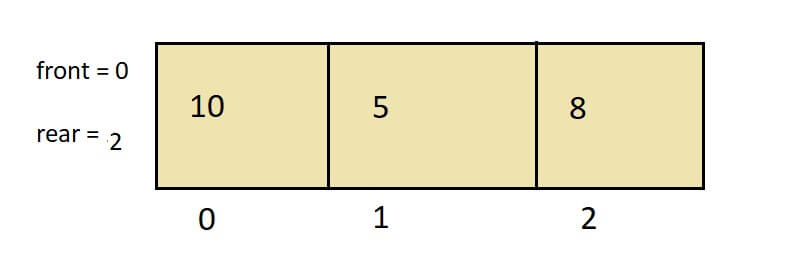
2. Enqueue (insertion): Suppose I want to insert the value “10”. But before the enqueue operation, check if the array size – 1 matches the value of the rear. (full() condition)

If yes, display an overflow message.
In our case, Array_size-1 is not equal to the rear. So increment the rear. So now increment the value of the rear from -1 to 0. my_queue[0] = 10 (my_queue[rear] = 10). This means at the 0^th position of the queue, the value is 10.

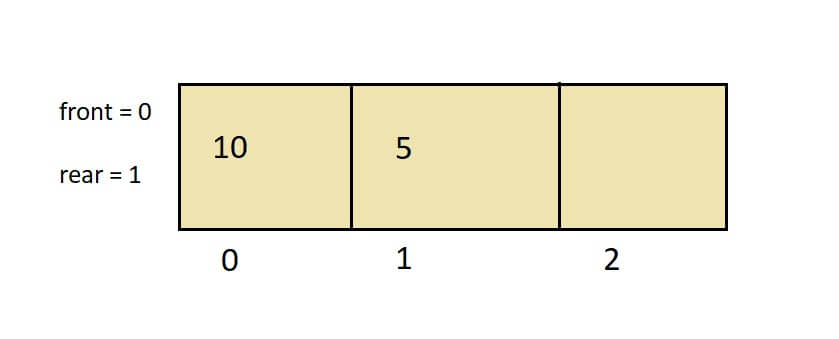
Now, I want to insert another element, “5,” in the queue. Check if rear == array_size – 1. It will return false. So increase the rear from 0 to 1 and insert queue[1] = 5.

Similarly, keep inserting; at one point, the rear value equals array_size – 1. This stage shows that the queue is complete, and if you try to do more increments, the whole condition will return true, and an overflow message will be displayed.

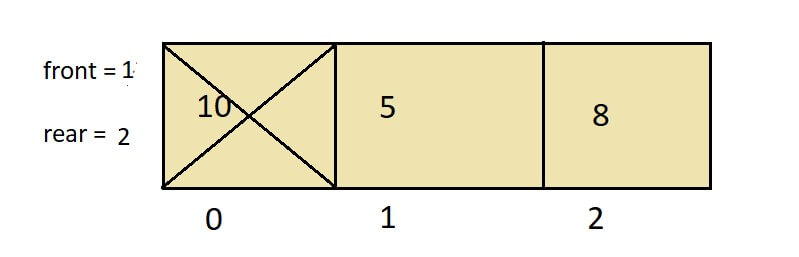
3. Dequeue: Since we have inserted three values in the queue, let’s see how to remove those three elements and empty the queue. Now, the front pointer is at 0 (after adding an element in the queue). So the front is not equal to -1 (isEmpty condition will return false). Hence, eliminate the item from position 0 of the queue.

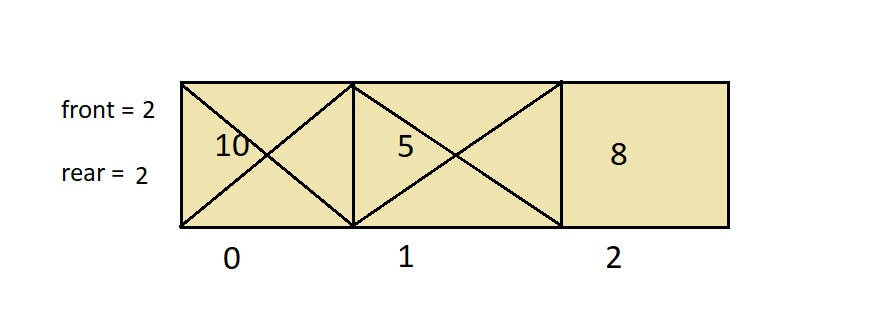
Check again for the isEmpty condition; it will return false. Increase the front value from 0 to 1, removing the element from the queue[front].

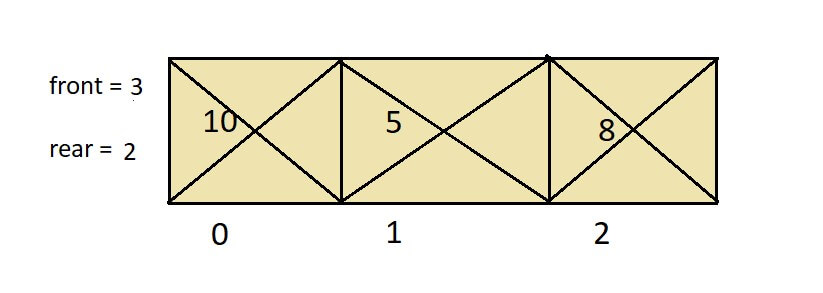
After removing the last element, the queue will be empty if we check the isEmpty condition. It will return true because when the front value becomes more significant than the value of the rear, they both will reset to -1.

In this way, the FIFO principle works in a queue using enqueue and dequeue.

Time Complexity

The array implementation of a queue’s time complexity factor is the time operations such as enqueue, dequeue, etc., take to execute in relation to the size of the array.

Enqueue: The time complexity in the insertion operation is 0(1); execution time does not change if the size of the array changes.
Dequeue: In the worst scenarios, the time complexity is 0(n) because when the elimination from the front position occurs, it might take some time to reposition all the elements concerning the front position.
Other operations like checking isEmpty and isFull have 0(1) time complexity.

Examples of Array Implementation of Queue

Here are the different examples of executing array implement of a queue using other languages:

Example #1 – Using JavaScript

Code:

class Queue {
constructor(queue_size) {
this.array_size = queue_size;
this.queueArray = new Array(queue_size);
this.front = -1;
this.rear = -1;
}
// Function to check if the queue is empty
isEmpty() {
return this.front === -1;
}
// Function to check if the queue is full
full() {
return this. rear === this.array_size - 1;
}
// Enqueue operation to insert an element to the rear position of the queue
queue_enqueue(element) {
if (this.isFull()) {
console.log("Queue is full. Cannot enqueue.");
return;
} else {
this.rear++;
this.queueArray[this.rear] = element;
console.log(`Enqueued element: ${element}`);
console.log(`Value of rear after inserting element: ${this.rear}`);
}
if (this.isEmpty()) {
this.front = 0;
}
}
// Dequeue operation to eliminate and return the element from the front position of the queue
queue_dequeue() {
if (this.isEmpty()) {
console.log("Queue is empty. Cannot dequeue.");
return;
}
const dequeuedElement = this.queueArray[this.front];
this.front++;
console.log(`Dequeued element: ${dequeuedElement}`);
console.log(`Value of front after inserting element: ${this.front}`);
if (this.front > this.rear) {
// If the value of the front becomes greater than the rear, reset the front and rear to -1 to indicate an empty queue
.front = -1;
this.rear = -1;
console.log(`value of front after resetting: ${this.front}`);
console.log(`value of rear after resetting: ${this.rear}`);
}
return dequeuedElement;
}
}
// Use the above functions with actual values.
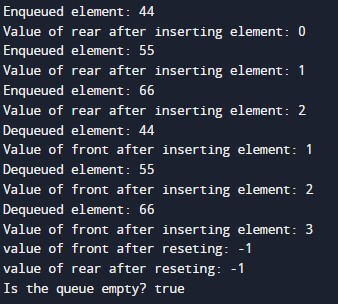
const queue = new Queue(5);
queue.queue_enqueue(44);
queue.queue_enqueue(55);
queue.queue_enqueue(66);
queue.queue_dequeue();
queue.queue_dequeue();
queue.queue_dequeue();
console.log("Is the queue empty?", queue.isEmpty());

Output:

Example #2 – Using Python

Code:

class Queue:
    def __init__(self, queue_capacity):
        self.array_size = queue_capacity
        self.queue_array = [None] * queue_capacity
        self.rear = -1
        self.front = -1
    def is_empty(self):
        return self.front == -1
    def is_full(self):
        return self.rear == self.array_size - 1
    def queue_enqueue(self, element):
        if self.is_full():
            print("Queue is full. Cannot enqueue.")
            return
        else:
            self.rear += 1
            self.queue_array[self.rear] = element
            print(f"Enqueued element: {element}")
            print(f"Value of rear after inserting element: {self.rear}")
        if self.is_empty():
            self.front = 0
    def queue_dequeue(self):
        if self.is_empty():
            print("Queue is empty. Cannot dequeue.")
            return
        dequeued_element = self.queue_array[self.front]
        self.front += 1
        print(f"Dequeued element: {dequeued_element}")
        print(f"Value of front after inserting element: {self.front}")
        if self.front > self.rear:
            self.front = -1
            self.rear = -1
            print(f"Value of front after resetting: {self.front}")
            print(f"Value of rear after resetting: {self.rear}")
        return dequeued_element
 # Use the above functions with numeric values.
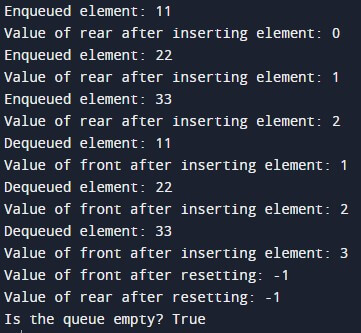
queue = Queue(5)
queue.queue_enqueue(11)
queue.queue_enqueue(22)
queue.queue_enqueue(33)
queue.queue_dequeue()
queue.queue_dequeue()
queue.queue_dequeue()
print("Is the queue empty?", queue.is_empty())

Output:

Example #3 – Using Java

Code:

public class Main {
  public static void main(String[] args) {
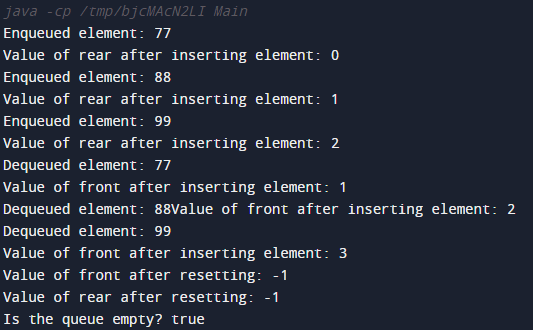
    Queue queue = new Queue(5);
    queue.queueEnqueue(77);
    queue.queueEnqueue(88);
    queue.queueEnqueue(99);
    queue.queueDequeue();
    queue.queueDequeue();
    queue.queueDequeue();
    System.out.println("Is the queue empty? " + queue.isEmpty());
  }
 }
 class Queue {
  private int arraySize;
  private int[] queueArray;
  private int front;
  private int rear;
  public Queue(int queueSize) {
    this.arraySize = queueSize;
  this.queueArray = new int[queueSize];
    this.front = -1;
    this.rear = -1;
  }
  public boolean isEmpty() {
    return front == -1;
  }
  public boolean isFull() {
    return rear == arraySize - 1;
  }
  public void queueEnqueue(int element) {
    if (isFull()) {
      System.out.println("Queue is full. Cannot enqueue.");
      return;
    } else {
      rear++;
      queueArray[rear] = element;
      System.out.println("Enqueued element: " + element);
      System.out.println("Value of rear after inserting element: " + rear);
    }
    if (isEmpty()) {
      front = 0;
    }
  }
  public int queueDequeue() {
    if (isEmpty()) {
      System.out.println("Queue is empty. Cannot dequeue.");
      return -1; // Return a special value or throw an exception to indicate an error
    }
    int dequeuedElement = queueArray[front];
    front++;
    System.out.println("Dequeued element: " + dequeuedElement);
    System.out.println("Value of front after inserting element: " + front);
    if (front > rear) {
      front = -1;
      rear = -1;
      System.out.println("Value of front after resetting: " + front);
      System.out.println("Value of rear after resetting: " + rear);
    }
    return dequeuedElement;
  }
}

Output:

Example #4 – Using C

Code:

#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 5
struct Queue {
int array[MAX_SIZE];
int front, rear;
};
// Function to initialize a queue
void initializeQueue(struct Queue *queue) {
queue->front = -1;
queue->rear = -1;
}
// Function to check if the queue is empty
int isEmpty(struct Queue *queue) {
return queue->front == -1;
}
// Function to check if the queue is full
int isFull(struct Queue *queue) {
return queue->rear == MAX_SIZE - 1;
}
// Enqueue operation to insert an element to the rear position of the queue
void enqueue(struct Queue *queue, int element) {
if (isFull(queue)) {
printf("Queue is full. Cannot enqueue.\n");
return;
} else {
queue->rear++;
queue->array[queue->rear] = element;
printf("Enqueued element: %d\n", element);
printf("Value of rear after inserting element: %d\n", queue->rear);
}
if (isEmpty(queue)) {
queue->front = 0;
}
}
// Dequeue operation to eliminate and return the element from the front position of the queue
int dequeue(struct Queue *queue) {
if (isEmpty(queue)) {
printf("Queue is empty. Cannot dequeue.\n");
return -1;
}
int dequeuedElement = queue->array[queue->front];
queue->front++;
printf("Dequeued element: %d\n", dequeuedElement);
printf("Value of front after inserting element: %d\n", queue->front);
if (queue->front > queue->rear) {
// If the value of the front becomes greater than the rear, reset the front and rear to -1 to indicate an empty queue
initializeQueue(queue);
printf("Value of front after resetting: %d\n", queue->front);
printf("Value of rear after resetting: %d\n", queue->rear);
}
return dequeuedElement;
}
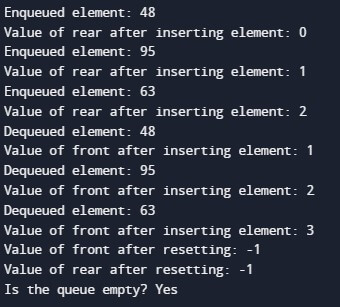
int main() {
struct Queue queue;
initializeQueue(&queue);
enqueue(&queue, 48);
enqueue(&queue, 95);
enqueue(&queue, 63);
dequeue(&queue);
dequeue(&queue);
dequeue(&queue);
printf("Is the queue empty? %s\n", isEmpty(&queue) ? "Yes" : "No");
return 0;
}

Output:

Example #5 – Using C++

Code:

#include <iostream>
class Queue {
private:
static const int MaxSize = 5;
int array[MaxSize];
int front, rear;
public:
Queue() : front(-1), rear(-1) {}
// Function to check if the queue is empty
bool isEmpty() {
return front == -1;
}
// Function to check if the queue is full
bool full() {
return rear == MaxSize - 1;
}
// Enqueue operation to insert an element to the rear position of the queue
void enqueue(int element) {
if (isFull()) {
std::cout << "Queue is full. Cannot enqueue." << std::endl;
return;
}
rear++;
array[rear] = element;
std::cout << "Enqueued element: " << element << std::endl;
std::cout << "Value of rear after inserting element: " << rear << std::endl;
if (isEmpty()) {
front = 0;
}
}
// Dequeue operation to eliminate and return the element from the front position of the queue
int dequeue() {
if (isEmpty()) {
std::cout << "Queue is empty. Cannot dequeue." << std::endl;
return -1;
}
int dequeuedElement = array[front];
front++;
std::cout << "Dequeued element: " << dequeuedElement << std::endl;
std::cout << "Value of front after inserting element: " << front << std::endl;
if (front > rear) {
// If the value of the front becomes greater than the rear, reset the front and rear to -1 to indicate an empty queue
front = -1;
rear = -1;
std::cout << "Value of front after resetting: " << front << std::endl;
std::cout << "Value of rear after resetting: " << rear << std::endl;
}
return dequeuedElement;
}
};
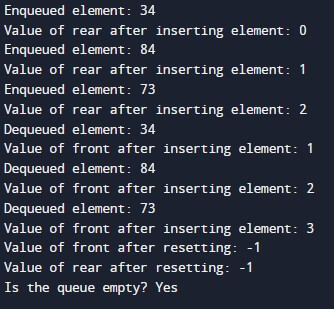
int main() {
// Use the Queue class
Queue queue;
queue.enqueue(34);
queue.enqueue(84);
queue.enqueue(73);
queue.dequeue();
queue.dequeue();
queue.dequeue();
std::cout << "Is the queue empty? " << (queue.isEmpty() ? "Yes" : "No") << std::endl;
return 0;
}

Output:

Example #6 – Using C#

Code:

using System;
public class Queue
{
private const int MaxSize = 5;
private int[] array = new int[MaxSize];
private int front = -1;
private int rear = -1;
// Function to check if the queue is empty
private bool IsEmpty()
{
return front == -1;
}
// Function to check if the queue is full
private bool IsFull()
{
return rear == MaxSize - 1;
}
// Enqueue operation to insert an element to the rear position of the queue
public void Enqueue(int element)
{
if (IsFull())
{
Console.WriteLine("Queue is full. Cannot enqueue.");
return;
}
rear++;
array[rear] = element;
Console.WriteLine($"Enqueued element: {element}");
Console.WriteLine($"Value of rear after inserting element: {rear}");
if (IsEmpty())
{
front = 0;
}
}
// Dequeue operation to eliminate and return the element from the front position of the queue
public int Dequeue()
{
if (IsEmpty())
{
Console.WriteLine("Queue is empty. Cannot dequeue.");
return -1;
}
int dequeuedElement = array[front];
front++;
Console.WriteLine($"Dequeued element: {dequeuedElement}");
Console.WriteLine($"Value of front after inserting element: {front}");
if (front > rear)
{
// If the value of the front becomes greater than the rear, reset the front and rear to -1 to indicate an empty queue
front = -1;
rear = -1;
Console.WriteLine($"Value of front after resetting: {front}");
Console.WriteLine($"Value of rear after resetting: {rear}");
}
return dequeuedElement;
}
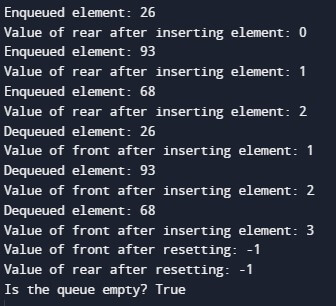
static void Main()
{
Queue queue = new Queue();
queue.Enqueue(26);
queue.Enqueue(93);
queue.Enqueue(68);
queue.Dequeue();
queue.Dequeue();
queue.Dequeue();
Console.WriteLine($"Is the queue empty? {queue.IsEmpty()}");
}
}

Output:

Applications of Queue

Queues are the most commonly used data structure in computer science.

Task scheduling: Due to its FIFO nature, tasks can be planned in a computer system using a queue.
Printing process: Printers print the document as the First in the first printed manner.
Call Center: The central system receives multiple calls and distributes them among the agents. The first call received will be the first one answered.
Buffer administration: Data flow between 2 processes is managed using a queue.
E-commerce: A queue data structure is used to manage orders. Orders received first are completed first.

These are some of the most common and easy-use cases of queue data structure.

Advantages and Disadvantages

Advantages

The queue has the most straightforward working mechanism, FIFO, that is easy to understand and implement. It aligns with many day-to-day use cases.
Applications such as task scheduling in computer systems, printers, call centers, etc., manage tasks in a FIFO (First In, First Out) manner.
Queue, being a data structure, can handle the data in a well-organized manner.
It can be integrated with many languages like C++, python, javascript, java, etc.
One of the fundamental operations in an operating system is processing, and processes use a queue to share data.

Disadvantages

You can only access the linear queue from the rear or front.
In some cases, the size of the queue is fixed. So, issues like overflow often tend to happen.
Handling underflow and overflow conditions is necessary.
Implementing a queue in multithreaded scenarios, where multiple threads execute within a single process, becomes complex.

Conclusion

A queue is one of the most straightforward data structures using the FIFO principle, and array implementation of a queue enhances the applications of the queue. Generally, two significant operations are carried out in a queue: Enqueue and Dequeue. Queue has made its place in multiple applications collaborating with different program languages. Hence, the queue and its array implementation have become crucial to the computer science stream.

FAQ’s

Q1. What is dynamic resizing in the Array implementation of the queue?

Answer: Dynamic resizing refers to enlarging or shrinking an array size as needed. This helps to avoid premature overflowing of the queue.

Q2. What is the disadvantage of defining a size at the initial stage?

Answer: If we define a large size at the initial stage, this may lead to memory wastage, and if we determine a tiny size, this may cause an overflow of the queue.

Q3. Can a double-ended queue be used in the array implementation of the queue?

Answer: Yes, it can be used as it can handle operations at both ends of the queue. In a double-ended queue, elements can be added or removed from the rear and front points.

Quiz Result
Total Questions	Correct Answers	Wrong Answers	Percentage

Introduction of Array Implementation of Queue

Table of Contents

Key Takeaways

What is a Queue?

Basic Operations on Queue

Algorithm for the Implementation of Queue Using Array

How to Implement Queue Using Array?

Time Complexity

Examples of Array Implementation of Queue

Example #1 – Using JavaScript

Example #2 – Using Python

Example #3 – Using Java

Example #4 – Using C

Example #5 – Using C++

Example #6 – Using C#

Applications of Queue

Advantages and Disadvantages

Conclusion

FAQ’s

Recommended Articles

Follow us!

APPS

Blog

Courses

Email