Updated June 21, 2023
Introduction to Armstrong Number in Python
A number is an Armstrong number if it equals the sum of its digits raised to the number of digits’ power. Let us understand Armstrong’s number by taking an example of a number. Let the number be n. Find out the number of digits in the number. Each digit in the number is taken and raised to the power n. All those are added together, and if the sum of all these numbers is equal to the number itself, then the number n is an Armstrong number. If not, the number n is not an Armstrong number.
How to Determine Armstrong Number in Python?
Let us understand the logic of how to determine the Armstrong numbers in Python.
- The input number is read using input().
- “We check the entered value to determine if it is an integer or not.
- We check the entered value to determine if it is greater than zero.
- Declare a variable and assign it to zero.
- We find each digit in the number using the modulus (%) operator to obtain the remainder of the input number.
- The cube of each digit is found and added to the initialized variable in step 4.
- The resulting number is floor divided by 10.
- Until the input number is not greater than zero, repeat steps 5,6, and 7.
- If the input number equals the initialized variable, the program will print the statement that the number is an Armstrong number.
- If the input number is not equal to the initialized variable, the program will print the statement that the number is not an Armstrong number.
All the single-digit numbers are Armstrong numbers because, in single-digit numbers, the value of a number of digits “n” is one, and anything raised to the power of one is the number “n” itself. Consider an example where the number is n=6.
6^1 = 6. Hence 6 is an Armstrong number. There are no two-digit Armstrong numbers. Consider an example where the number n=22.
2^2 + 2^2
=4 + 4
=8
In the above example, the number n=22 is not equal to the sum of its digits raised to the number of digits’ power. Hence n is not an Armstrong number. There are four three-digit Armstrong numbers. Consider an example where the number is n=371.
3^3 + 7^3 + 1^3
=27 + 343 + 1
=371
In the above example, the number n=371 equals the sum of its digits raised to the number of digits’ power. Hence n is an Armstrong number. There are two four-digit Armstrong numbers. Consider an example where the number is n=1634.
1^4 + 6^4 + 3^4 + 4^4
=1 + 1296 + 81 + 256
=1634
In the above example, the number n=1634 equals the sum of its digits raised to the number of digits’ power. Hence n is an Armstrong number.
Examples to determine Armstrong Number in Python
Let us see some examples to determine Armstrong number in PPython, which are given below:
Example #1
Let us understand how to determine Armstrong’s number in a Python programming language using the if-else statement.
Code:
# input is taken from the user
number = int(input("Please input a number "))
# Variable result is initialized
result = 0
# cube of each digit is added to find the sum
temporary = number
while temporary > 0:
digit = temporary % 10
result += digit ** 3
temporary //= 10
# result is displayed
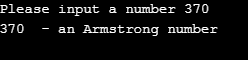
if number == result:
print(number," - an Armstrong number")
else:
print(number," - not an Armstrong number")Output:
The output of the above program with input as 1234,
Example #2
Let us understand how to determine Armstrong’s number in the Python programming language using a list.
Code:
# Program to check Armstrong numbers using list
number=int(input("Please input any number: "))
number1=list(map(int,str(number)))
number2=list(map(lambda x:x**3,number1))
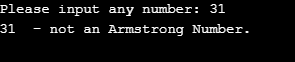
if(sum(number2)==number):
print("The given number is an armstrong number. ")
else:
print("The given number isn't an arsmtrong number. ")Output:
The output of the above program with input as 542,
Example #3
Let us understand how to determine Armstrong’s number in a Python programming language using a recursive function.
Code:
# Program to check Armstrong numbers using recursive function
# getSum() recursive function is defined
def getSum(number):
if number == 0:
return number
else:
return pow((number%10),order1) + getSum(number//10)
# storing the input in number variable
number = int(input("Please input any number: "))
# len() and str() function is used to find the order
order1 = len(str(number))
# getSum() gives the sum and the sum variable is initialised
sum = getSum(number)
# the sum is equal to number or not is checked
if sum == int(number):
# Determining if the number is an Armstrong number
print(number," - an Armstrong Number.")
else:
# Determining if the number is not an Armstrong number
print(number," - not an Armstrong Number.")Output:
The output of the above program with input as 1634,
Conclusion
In this article, we have learned Armstrong numbers in PPython, logic to determine Armstrong numbers, and various Python programs using if-else statements, recursive functions, for loops, and lists to check whether a given number is an Armstrong number. This article will help the readers trace the programs written in PPython to determine if a given number is an Armstrong number.
Recommended Articles
This is a guide to Armstrong Number in Python. Here we discuss how to determine Armstrong Number in Python, examples, and code implementation. You can also go through our other related articles to learn more –