What is Armstrong Number in Java?
Armstrong Number in Java Armstrong is one in which the sum of the cubes of the individual digits of the number is equal to the number itself. Armstrong number is a special kind of number where the digits are first picked up, then they are cubed, and finally, all the cubes of the individual digits are added to get a number. If the number thus found is equal to the original number, then the respective number is known as an Armstrong number. An example of Armstrong’s number is 153. If we break down the digits of 153, they are 1, 5 and 3. Then we find the cube of the respective numbers, and finally, we calculate the cube of the numbers.
153= (1*1*1)+(5*5*5)+(3*3*3)
370= (3*3*3)+(7*7*7)+(0*0*0)In this way, we can calculate whether a number is an Armstrong number or not.
Examples of Armstrong Number in Java
We will see the illustration with the help of examples.
Example #1
In the coding example, we use Java programming language to determine whether the number is an Armstrong number or not. If the entered number is an Armstrong number, then the program automatically prints it is as an Armstrong number, and if it is not one, it replies automatically that the number is not an Armstrong number. We can enter three-digit or four-digit values to check whether the number is an Armstrong number or not.
The program’s logic is such that each digit of the respective number is stored in the temp variable. Then, the number is cubed to find out the respective digit’s cube, which is stored in another variable total. Finally, the total number is checked with the corresponding original number. The digits are obtained one by one by getting the number divided by 10 at each step, then getting the remainder of the number, and then cubing the number to get the respective digit’s cube.
Code:
import java.io.*;
public class Armstrong
{
public static void main(String[] args)throws IOException
{
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
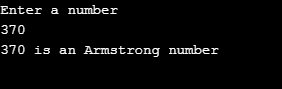
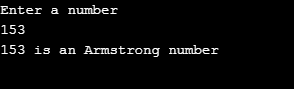
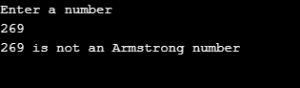
System.out.println("Enter a number");
int num = Integer.parseInt(br.readLine());
int number, digit, sum = 0;
number = num;
while (number != 0)
{
digit = number % 10;
sum = sum + digit*digit*digit;
number /= 10;
}
if(sum == num)
System.out.println(num + " is an Armstrong number");
else
System.out.println(num + " is not an Armstrong number");
}
}Output:
In the first program, we enter the numbers 370 and 153 as numbers to check whether they are Armstrong or not. Also, we enter 269 as a number to check whether the number is Armstrong. We get the program’s respective output that the numbers 370 and 153 are Armstrong numbers while the number 269 is not an Armstrong number.
Example #2
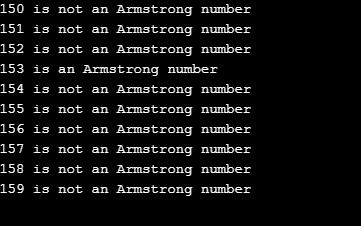
In the second coding example, we select a range of numbers that are checked whether they are Armstrong numbers or not. The range is from 150 to 160. We select the range, and we check the output whether the number is an Armstrong number or not. Then we see the output. The logic used is similar to that of the logic used for finding an Armstrong number. The respective digits of the number are calculated, and then they are cubed and summed to find the final total number. If the final total number is equal to the original number, they are regarded as Armstrong numbers calculated.
Code:
import java.io.*;
public class ArmstrongRange
{
public static void main(String[] args)throws IOException
{
for(int num= 150; num<160; num++)
{
int number, digit, sum = 0;
number = num;
while (number != 0)
{
digit = number % 10;
sum = sum + digit*digit*digit;
number /= 10;
}
if(sum == num)
System.out.println(num + " is an Armstrong number");
else
System.out.println(num + " is not an Armstrong number");
}
}
}Output:
In the sample output, we see that all the numbers in the range of 150 to 160 have been checked for whether they are Armstrong numbers or not. The program has reported that only 153 is an Armstrong number whose sum of cubes of digits is equal to the original number. All the other numbers have been reported as non-Armstrong numbers.
Example #3
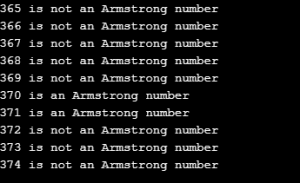
In this coding example, we will see the list of Armstrong numbers present between 365 and 375. We are changing the range of the values to be checked for Armstrong numbers. The sample logic of the coding is exactly the same as the previous ones. The main difference is that the range of numbers to be checked is changed, and they are slightly different from the last line of code.
The individual digits are taken, cubed and summed to get a number. If that number is the same as the original number, then the original number is known as an Armstrong number; otherwise, it is not an Armstrong number.
Code:
import java.io.*;
public class ArmstrongRange
{
public static void main(String[] args)throws IOException
{
for(int num= 365; num<375; num++)
{
int number, digit, sum = 0;
number = num;
while (number != 0)
{
digit = number % 10;
sum = sum + digit*digit*digit;
number /= 10;
}
if(sum == num)
System.out.println(num + " is an Armstrong number");
else
System.out.println(num + " is not an Armstrong number");
}
}
}Output:
In the program’s sample output, we see that only 371 and 370 are Armstrong numbers while the other numbers are not as the sum of the cubes of the individual digits does not add up to the original number.
Conclusion – Armstrong Number in Java
In this article, we have seen the working and definition of an Armstrong number. First, we check whether a number entered is an Armstrong number or not. Secondly, we input a range of values from 150 to 160 and check how many Armstrong numbers are there in between those values. Thirdly, we input a range of numbers from 365 to 375 and find out that 370 and 371 are Armstrong numbers. Armstrong numbers are special numbers used in number theory and can be used to find the nature of digits of some numbers and the summation of their cubes.
Recommended Articles
This has been a guide to the Armstrong Number in Java. Here we how to illustrate the Armstrong number in Java with the help of few examples. You may also have a look at the following articles to learn more–