Introduction to Types of Vectors
A vector is a mathematical concept representing a quantity with both magnitude and direction. It is commonly depicted as a directed line segment, where the length corresponds to the magnitude of the vector, and the orientation indicates its direction. Vectors find extensive application in various fields of mathematics.
Top 10 Types of Vectors
There are different types of vectors.
1. Co-initial Vectors
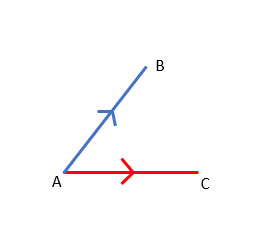
The co-initial vectors are vectors in which two or more separate vectors have similar initial points. In this type of vector, all vectors originate from the same position. The vectors AB→ and AC→ have a similar initial point, which is A, so we call them co-initial vectors.
2. Collinear Vectors
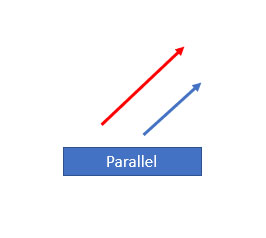
The collinear is the other type of vector in which there are two or more two vectors are parallel to each other irrespective of the magnitude or the direction. The parallel in nature means they never intersect with each other. The direction of both vectors is the same in nature. For example, if vector a is in the x-direction and b is in the same direction, they are known as collinear vectors. The coordinates of both vectors are the same in nature. The other property of a collinear vector is that the cross product of both the collinear vectors is always equal to zero. The other name for collinear vectors is parallel vectors.
3. Zero Vector
The zero vector is another type of vector in which the vector magnitude is equal to zero, and the origin point of the vector coincides with the terminal point. For example, if the vector AB-> if the coordinates of A and the coordinates of B are the same, then the vector is known as zero vector. The direction of the zero vector is indeterminate, and the magnitude is always zero. The zero vector does not point in any direction and also has all components equal to zero.
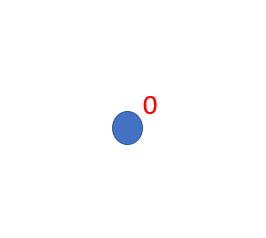
In the above diagram, the zero vector is shown above.
4. Unit Vector
The unit vector is the type of vector that has a magnitude equal to the unit length that is one. Suppose there is a vector x-> with the magnitude x, then the unit vector is shown by x̂ that has the same direction as vector x and magnitude one.
![]()
5. Position Vector
The vector OA-> is known as the position vector having the reference origin 0.
6. Co-planar Vectors
The co-planar vectors are the type of vectors in which three or more than three vectors lie in the same plane or can lie in the parallel plane. The other property for co-planar vectors is the scalar triple product for the three vectors is always equal to zero. The co-planar vectors are always linearly dependent vectors.
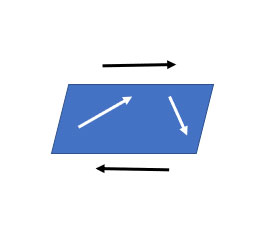
7. Like and Unlike Vectors
Like vectors are vectors that have the same direction. On the other hand, unlike vectors are vectors with opposite directions, regardless of each other.
8. Equal Vector
Equal vectors are vectors in which two or more vectors have the same magnitude and the same direction.
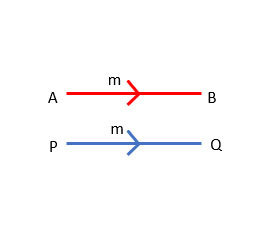
In the above diagram, the vectors AB-> and PQ-> are equal vectors as they have the same magnitude and direction.
9. Displacement Vectors
The displacement vector is the type of vector. For example, if there is any object that is present at point A at time =0 and after some time it is at point B at time =t.
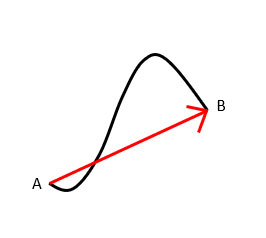
The direction is from point A to point B.
10. Negative Vector
The negative vector is the type of vector in which the two vectors have an equal magnitude, but the direction of both vectors is opposite. Suppose we have two vectors, a and b, which are negative vectors.
![]()
Conclusion
The vectors are the physical quantity that has the magnitude as well as the direction. Vectors are a mathematical concept, and there are various kinds of vectors like collinear vectors, coplanar vectors, like and unlike vectors, displacement vectors, unit vectors, and many more defined above.
Recommended Articles
This is a guide to Types of Vectors. Here we discuss the top 10 Types of Vectors in detail understanding. You can also go through our other related articles to learn more –

