Updated March 6, 2023
Definition of Trie Data Structure
Trie Data Structure is defined as a type of data structure that enables quick and efficient retrieval of a string from a bag consisting of a lot of other strings. These strings are signified as keys, and it is the way the strings are stored that makes the search an efficient and quick one. The word trie is derived from the method the data structure follows “reTRIEval.” Here the search complexity is reduced to the most optimal complexity, and the complexity is equal to the length of the search word. Even in cases of the optimal and well-balanced binary trees, the time complexity is of the order of M * log (N), where M signifies the length of the search string and N signifies the total number of keys in the binary search tree. Here in this article, we will look at the algorithm of Trie Data structure and also understand some of its advantages and disadvantages.
Trie Data Structure Algorithm
Firstly, we need to understand the construction of a trie data structure before we even move on to understanding the operations in Trie data structure and its algorithms. A trie data structure depicts a tree where each node represents a character if a string is stored and single digits in case a number is stored, and the very first node is an empty node which is denoted as a root node. From each of those nodes, there is a possibility of different branching of characters depending on what word is stored. For example, if ordered and order are the two words that are stored, then alphabetically, both the words have commonality till order. Now at the node “r,” which is the last alphabet of the word order, there will be 2 branches where one branch will denote the word ordered and the other ordering, essentially meaning that from the alphabet “r” one branch will have “ed” and the other “ing.” The next thing about the structure is that the last alphabet of any word stored is flagged with a digit or any desired flag to mention that the word has ended at this character.
Now that we know the structure of a trie data structure and proceeding ahead to fully under the algorithm of trie data structure, we need to understand the different operations that are accomplished by Trie data structures. These operations insert, search and delete, and hence in order to understand the algorithm of Trie data structure, it is important to understand the individual algorithms of the operations that are possible using Trie data structure.
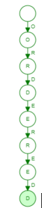
To begin with, we first look at the insert operation in the Trie data structure. From our earlier discussion points, we saw that every node of a trie data structure might contain various branches and also that we flag the last node of every word which are stored in the data structure. With this knowledge, we know that at first, the trie data structure is an empty one. Now, when the first word is inserted, each of the alphabets is stored as a node. For example, let us take the earlier examples, ordered and ordering. Let us suppose we insert the word ordered; this is how it will look like. How it happens is that each alphabet of ordered passes through the first O, then R, then D, then E, and so on till final alphabet, which is D.
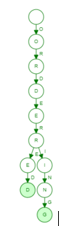
Now, once this structure is built, as we insert the second word, i.e., ordering, the algorithm will start from the root node, and each alphabet of the next word will start to flow in, and the algorithm will see if there is a similar trail already existing. If there is a similar trail existing, the alphabets of the word will keep following the trail till the point the word starts being different from each other. Now since ordered is already existing in the chain, till the word order, it will follow the same trail, and from the next word, it will branch out. The way is depicted below:
Carefully note that the last alphabet has a different color, i.e., depicting that the last word is the end alphabet of the word. There might be cases when starting alphabet is different, and hence the branch starts from the root node something like (The word inserted is Educba):
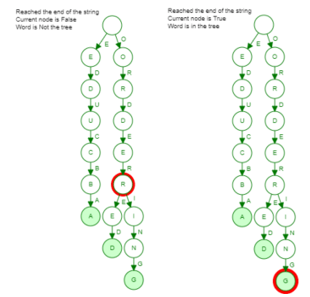
Now, in order to search for a word, similar to the case it was inserted, the individual alphabets are passed on and then looked for in the tree, which stores the pool of strings. Now, if the tree already has a word, it returns that the word is present. Now, the way the strings are stored, some substrings can also be present, and hence the tree might return that a substring is present. For example, if we search order, then we see that it is present, but not as a string but as a substring. This is where the flag of being the end alphabet is checked, and if the last alphabets of the search string are also the flagged alphabet, we say that the word is present, else not. Below are 2 cases where in the first figure, we say that order is NOT present, and in the second figure, we say that the word order is present.
For deletion, we need to follow the below process:
1. Search for the word to be deleted and then:
a. If the word that needs to be deleted is not present, the trie is not modified at all.
b. If the word is not a suffix or prefix to any other word, and the individual nodes are also not branched, delete all nodes from root to leaf (last) node.
c. If the word to be deleted is a prefix to another word, then the leaf node, which is the last alphabet of the word to be deleted, is flagged as not end alphabet.
d. If the word to be deleted is a suffix to some other word (w1), then all nodes of a word that are not a part of the w1 are deleted.
e. Finally, if none of the above happens and the word to be deleted is neither a prefix or a suffix, but some nodes are just shared with another word, then the uncommon alphabets should be deleted.
Advantages and Disadvantages of Trie data structure
Advantages:
1. The insert and the search algorithm have the best time complexity, i.e., O(n), faster than even the best of BST.
2. All words can be easily printed in alphabetical order, which is difficult if we use hashing.
3. Prefix search is easily doable.
Disadvantages:
1. A lot of memory is used in storing the pool of strings in a Trie, and as more and more words are inserted, space complexity explodes.
Conclusion
In this article, we looked at all the algorithms that concern a Trie DS along with Trie’s advantages and disadvantages which will enable readers to make informed decisions while choosing Trie and also while using them as well.
Recommended Articles
This is a guide to Trie Data Structure. Here we discuss the Introduction, Trie Data Structure Algorithm, Advantages, and disadvantages. You may also have a look at the following articles to learn more –

