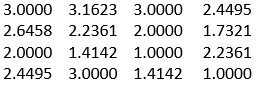Updated March 24, 2023
Introduction to Square Root in Matlab
Square root is defined as taking the root of any square of a single element, a matrix or an array. Square root of a number can be positive or negative as a square of a positive number is positive and the square of a negative number is also positive. It is denoted by √ the symbol. Square root is simply the inverse method of squaring. If a^2 is the square integer, then a is defined as the square root of that number.
For example, 16 is a perfect square number and its square root can be 4 or -4. There are many methods that are used in mathematics to find the square root of a number.
Working and Uses of Square Root in Matlab with Examples
Matlab performs all mathematical functions, so there are also methods to find the square root of a number. In Matlab, we use the sqrt () function to find the square root of a number or each element defined in an array. The input arguments that are used in the function can be scalar, vector, array or multi-dimensional array. They can also be positive, negative or complex in nature. If the input is complex or negative in nature, then it results in a complex number.
Syntax:
Y = sqrt(x)
Example #1
Y = -3:3
So, the input is in the form of 1*7.
-3 -2 -1 0 1 2 3
A=sqrt(Y)
Output:
(0.0000 + 1.7320i) (0.0000 + 1.4142i) (0.0000 + 1.0000i) (0.0000 + 0.0000i) (1.0000 + 0.0000i) (1.4142 + 0.0000i) (1.7320+0.0000i)
Example #2
Y = -5: -3
So the input is in the form of 1*4
-5 -4 -3
A = sqrt(Y)
Output:
(0.0000+2.2360i) (0.0000+2.0000i) (0.0000+1.7320i)
We know that is the input of an array is negative than it results in a complex number. In the above two examples, we see that the range consists of negative and positive numbers, so the output of it is a complex number. Some operations differ in Matlab as compared to IEEE standard like the square root of negative zero is 0 in Matlab while it is -0 in IEEE, square root of values less than zero results in a complex number in Matlab while the same is not available in IEEE.
If we want to find the square root of only positive integers in an array, then we can use realsqrt () function in Matlab. Unlike sqrt () function, it gives error messages when we pass input as a negative or complex number. So, if we want to view the result of a negative or complex number than it is preferable to use sqrt () function. The output size and input size should be the same if we use realsqrt ().
Example #3
Input is a 4*4 matrix named as A
Y=realsqrt(A)
Output:
In the above example, it produces the square root of each element in a matrix. The input arguments can be a matrix, array, vector, scalar, or a multi-dimensional array and they should be positive and real integers. There are various properties of a square root in Matlab which should be noted:
The square root of any even number that is a perfect square should always be even.
For example: 16,36,64,100 etc.
Here 16, 36, 64 and 100 are all even numbers that are a perfect square and the square root of those numbers are 4,6,8 and 10 which are also even numbers.
The multiplication of square roots of the same number results in a positive integer while square roots of the number can also be multiplied and provide the output.
For example: √4 * √4 = 4
√3 * √2=√6
The square root of any odd number that is a perfect square should always be odd.
For example: 25,9,49,81
Here 25,9,47,81 are all perfect squares of odd numbers and the square root of those numbers are 5,3,7,9 which are also odd numbers. The unit digit of an element cannot be 3,2,8 or 7 to be a perfect square.
Conclusion
Square roots are widely used in Matlab for various business requirements. They are widely used in solving the solutions of any quadratic equations, machine learning topics like calculating standard deviation and variance. So, it is an essential feature in all the mathematical domains.
Recommended Articles
This is a guide to Square Root in Matlab. Here we discuss the working and uses of square root in Matlab with examples. You can also go through our other suggested articles to learn more –