Updated March 21, 2023
Introduction to Inline Function in Matlab
Inline Functions in Matlab have two categories one is inbuilt functions and the second is used defined functions that are created by the user.
Inbuilt Functions
Matlab has many built-in functions square root, sin, cos, tan, exponential, log, etc. It also has more complex and special mathematical functions like gamma functions and Bessel functions. It also has some built-in constants pi, I (complex numbers) and infinity.
Example:
sin ( pi / 2 )
It gives output as 1.
in this example we did not even mention the value of pi, automatically pi takes the value 3.14.
sqrt (3)
It gives output 1.73.
And if write program statement sqrt ( -1 ) it will give ans as 0.00 + i
User Defined Functions
The keyword is used to define our own function is “ inline ”, now let see how to use it
Let us assume I want to create one function fun = x ^ 2 – 6
Matlab commands will be
Fun = inline ( ‘ x ^ 2 – 6 ’ , ’ x ’ ) . . . . . . . . . . (1) function declaration and defination
Fun =
inline function :
Fun= – 6. . . . . . . output of (1)
Fun ( 1 ) (2) giving value x=1
Ans =
-5. . . .output of(2)
Fun ( 2 ) ....(3) giving value x=2
Ans =
-2 . . . output of(3)
Fun ( 3 ) . . . . . . . . . . . . . . . . . . . . (2) giving value x=3
Ans=
3. . . . . . . output of(3)
- Matlab functions operate on scalar as well as vectors
- To make inline function victories, the ‘ vectorize ’ keyword is used inside the function definition.
- In the above example suppose I want to create vector function ‘fun’ then commands will be
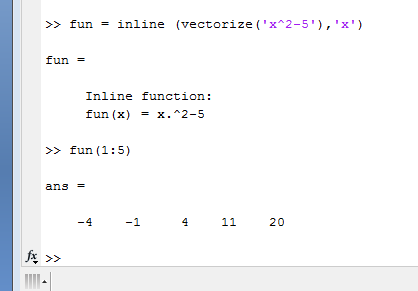
Fun = inline ( vectorize ( ‘ x ^ 2 – 5 ’ , ’ x ’ )
It will create vector fun.
Fun ( 1 : 5 )
And evolution will take values of x as 1 , 2 , 3 , 4 and 5
Output for this program will be
-4 -1 4 11 and 20
In this first value is for x = 1 , second value is for x = 2 , third value is for x = 3 , forth value is for x = 4 and fifth value is for x = 5.
Syntax of Inline Function
It is categorized into three parts:
1. Function Definition: In this, we write the function string and define the independent variable.
Function name = inline ( ‘ function ’ , ’ independent variable ’ )
Fun = inline ( ‘ x ^ 2 – 5 ’ , ’ x ’ )
2. Function Evolution: In this, we evaluate function by giving any value to the independent variable.
Function name (variable value )
Fun ( 1 )
3. Vectorize function: This function creates a vector of given function.
Function name = inline ( vectorize( ‘ function string ’ ) , ’ independent variable ’ )
Y = inline ( vectorize ( ‘ x ^ 2 – 1 ’ ) , ’ x ’ )
Examples
The following examples are as follows
Example #1
Let us consider one function
Z = x3 - 56
To solve the above equation in Matlab, we need to create an inline function for z and need to assign one independent variable.
Matlab code:
>>
z =
Inline function :
Z ( x ) = x . ^ 3 - 56
>> z ( 0 )
Ans = 4
>> z ( 1 0 )
Ans = 996
>> z ( -1 )
Ans = 5
Example #2
Z = x ^ 3 + 23 x - 9
Matlab code for example 2
Z = inline ( vectorize ( ' x .^3 + 23*x – 9 ' ) ,' x ' )
z =
Inline function :
Z ( x ) = x . ^ 3 + 23 * x - 9
>> z ( 1 : 10 )
Ans = Columns 1 through 3
15 45 87
Columns 4 through 6
147 231 345
Columns 7 through 9
495 687 927
Column 10
1221
>> z ( 1 : 0.5 : 5 )
Ans = Columns 1 through 4
15.0000 28.8750 45.0000 64.1250
Columns 5 through 8
87.0000 114.3750 147.0000 185.6250
Column 9
231.0000
Conclusion- Inline Functions in Matlab
Inline functions are global but it never takes any space in Matlab workspace. It works like anonymous functions but these are not anonymous functions because anonymous functions occupy space at the time of function creation. Inline functions return only one value though a system dealing with arrays and matrix.
Recommended Articles
This is a guide to Inline Functions in Matlab. Here we discuss Inline functions in Matlab, Syntax, and Examples. You can also go through our other related articles to learn more-