Updated March 13, 2023
Introduction to Sparse Matrix Multiplication
The following article provides an outline for Sparse Matrix Multiplication. Sparse matrix is the matrix in which most of the elements are zero. To store all the elements of the matrix leads to a wastage of memory. So it is better to store the data of only those elements which are non-zero in the existing matrix. For example, let’s suppose there is a matrix A of which most the element is 0. So, to store all the matrix, it is better to store only those elements which are non-zero. Using this way to store the matrix reduces the space and takes lesser time to perform operations. One of the operations is the multiplication of two matrixes, in which we multiply the two sparse matrices.
Syntax of Sparse Matrix Multiplication
To multiply two matrixes in which most of the elements is zero elements, Sparse matrix multiplication is used for better time complexity and space complexity. In sparse multiplication, it limits the processing time and space usage; instead of storing a lesser number of non-zero elements in a matrix, to store the elements that are non-zero, we use the below 2 representations.
1. Array Representation: An array representation where we need to access the elements more often. Since array store, the elements based on the indices thus is much helpful. The 2D array is converted to a 1D array with 3 columns representing.
- Row: Row index of the non-zero element.
- Column: Column index of non-zero element.
- Value: Value at the same row, column index in the 2D matrix.
2. Linked List Representation: In a linked list where the frequency of insertion and deletion operation in the matrix is more since it is easier to delete and insert elements in a linked list as compared to the arrays.
Each node has four fields as given below:
- Row: Row index of the non-zero elements in the matrix.
- Column: Column index of the non-zero elements in the matrix.
- Value: Value of the non-zero element at (row, column) position in the matrix.
- Next Node: Reference to the next node.
How to Perform Sparse Matrix Multiplication?
- A sparse matrix is the type of 2 -D matrix where zero elements are large compared to non-zero elements. And to multiply sparse matrixes takes a lot of memory space and time, and also it is difficult to perform any further operation. So to multiply these matrixes with less time and space storage, we can directly multiply two reduced sparse matrixes.
- Let’s suppose we have two matrixes, both contains most elements 0, to the multiplication of those matrix takes a lot of time means high time complexity and also it will be large space as well for storing 3 matrixes, so it is better to convert those matrixes into reduce the form of sparse matrix and multiply them and get the resultant matrix as a reduced the form of a sparse matrix as well, that multiplication is called Sparse Matrix Multiplication.
- We can also store the resultant multiplication matrix in the same as the above representation.
Example of Sparse Matrix Multiplication
Given below are the example of Sparse Matrix Multiplication:
Let us illustrate the concept of sparse matrix multiplication with an example.
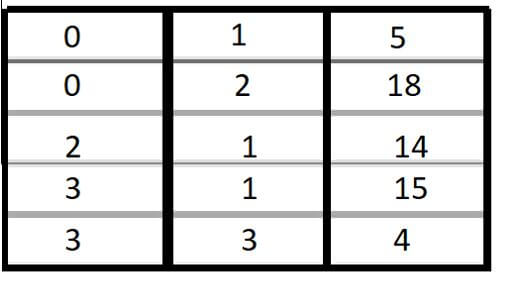
Consider below 2-D matrix with 4 rows and 4 columns.
So here, as we can see, only 5 elements out of 4 * 4 = 16 elements in the matrix are non-zero. So that depicts that we just need to store these 5 elements to store in the memory. So we just store the location of non-zero elements and their values.
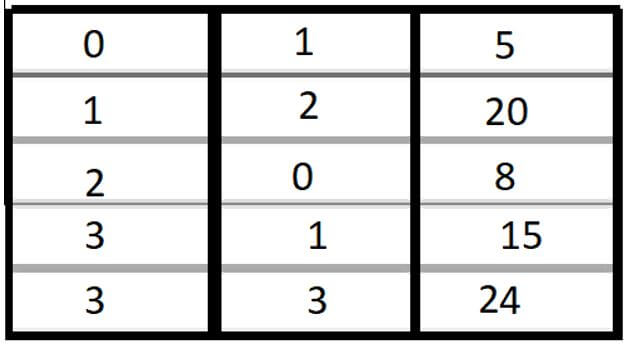
For multiplication, Let’s take another sparse matrix of 4*4 size.
So, here we can see that 5 elements have non-zero values.
To multiply them, we have to follow these steps:
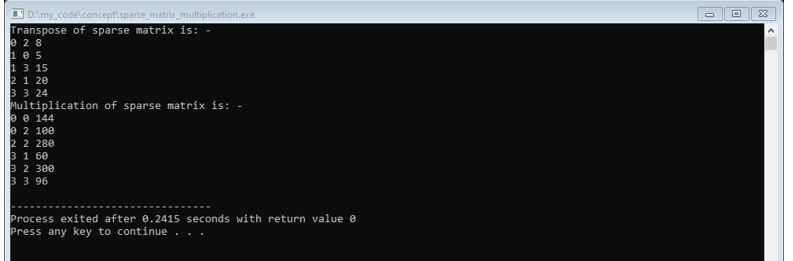
Step 1: First, we have to take the transpose of the second matrix. The transpose of a matrix is, converting all the rows into columns and columns to rows. So here as we store only non-zero elements. So we have to replace the rows with columns and columns with rows.
Step 2: So, in a resultant matrix of multiplication of these two matrixes, let x is a row of the first matrix and y is the row of the transpose of the second matrix, we get resultant[x][y]. For resultant[x][y] is the summation of all values, get after the multiplication of those values in which the column in the first matrix and column in the transpose of the second matrix is the same.
Step 3: Let x=0 and y=0; in the first matrix, two values are there in which row is 0 and one in the second matrix. So, if their column is also the same, then we multiply both and find another pair. So, in that example, in the first matrix, 0,2 value is 18, and in the second matrix, 0,2 is 5. So we multiply both and find another pair, but as we can see, there is no other pair in which column is the same. So, resultant [0][0] is 144.
Step 4: Follow step 3 for every 0<=x<row and 0<=y<column where resultant [x][y] is resultant matrix.
Code:
struct matrix {
int row; //To store row no.
int col; //To store col no
int value; // element value
};
// Print the sparse matrix
void printMatrix(matrix a[100], int k) {
for (int i=0; i<k;i++) {
cout << a[i].row <<" "<< a[i].col <<" "<< a[i].value << endl;
}
}
// Sort the sparse matrix
bool compareMatrix( struct matrix a, struct matrix b ) {
if (a.row < b.row) {
return true;
}
if (a.row > b.row) {
return false;
}
if (a.col < b.col) {
return true;
}
return false;
}
// Transpose of a sparse Matrix
void transpose(matrix a[100], matrix b[100], int row,int col, int n) {
for (int i=0;i<n;i++) {
b[i].row = a[i].col;
}
for (int i=0;i<n;i++) {
b[i].col = a[i].row;
}
for (int i=0;i<n;i++) {
b[i].value = a[i].value;
}
sort(b,b+n,compareMatrix);
cout << "Transpose of sparse matrix is: -" << endl;
printMatrix(b, n);
}
void multiply(matrix a[100], matrix transposeB[100], matrix resultant[100], int n1, int n2, int rows, int cols) {
int i = 0;
int j = 0;
int k = 0;
int temp = 0;
while( i<rows || j<cols ) {
int a1 = a[i].row;
int b1 = transposeB[j].row;
int tempi = i;
int tempj = j;
while( a[tempi].row==a1 ) {
tempj=j;
while( transposeB[tempj].row == b1) {
if(a[tempi].col == transposeB[tempj].col ) {
temp = temp + (a[tempi].value * transposeB[tempj].value);
}
tempj++;
}
tempi++;
}
if(temp != 0) {
resultant[k].row=a[i].row;
resultant[k].col=transposeB[j].row;
resultant[k].value=temp;
k++;
}
temp=0;
while(j<cols && b1==transposeB[j].row) {
j++;
}
if(b1==transposeB[j].row) {
while(i<rows && a1==a[i].row) {
i++;
j=0;
}
if(a1==a[i].row){
break;
}
}
}
cout << "Multiplication of sparse matrix is: -" << endl;
printMatrix(resultant,k);
}
int main() {
int row1=4, col1=4;
int row2=4, col2=4;
int n1=5,n2=5;
matrix a[n1]={
0,1,5,
0,2,18,
2,1,14,
3,1,15,
3,3,4
};
matrix b[n2] = {
0,1,5,
1,2,20,
2,0,8,
3,1,15,
3,3,24
};
matrix transposeb[n2];
matrix resultant[100];
transpose(b, transposeb, row2, col2, n2);
multiply( a, transposeb, resultant, n1, n2, row1, col2);
}
Output:
Conclusion
Sparse matrix multiplication is the solution to perform the multiplication of two matrixes in less time complexity. However, the resultant matrix is also having the most elements value 0, so it is better to store the resultant matrix in the same way. Thus, we can save a lot of space by storing just non-zero elements.
Recommended Articles
This is a guide to Sparse Matrix Multiplication. Here we discuss the introduction, how to perform sparse matrix multiplication? and example. You may also have a look at the following articles to learn more –