Updated March 29, 2023
Introduction to Sort Array 0s, 1s and 2s
When working with arrays, sorting them in a specific way is often necessary. One common problem is Sort Array 0s,1s, and 2s. In this, the problem can be solved in linear time (i.e., O(n)) and constant space (i.e., O(1)) using a technique called the “Dutch National Flag Algorithm.” The algorithm works by maintaining three-pointers that divide the array into three sections: the low section for 0s, the midsection for 1s, and the high section for 2s. The algorithm traverses the array once and swaps the elements to group them into their respective sections. The goal is to rearrange the elements of the array so that all the 0’s come first, followed by all the 1’s, and then all the 2s.
This may seem simple at first glance, but it can be challenging to do efficiently when dealing with large arrays. There are several methods for sorting this type of array, each with its own advantages and disadvantages. In this article, we will learn and explore some methods and discuss an optimized approach using three-way partitioning with single traversal.
Definition
Basically, Sort Array 0s,1s, and 2s means arranging the elements of the array such that all the 0s appear before the 1s and all the 1s appear before the 2s. The problem of sorting such an array involves arranging the elements of the array in ascending order such that all the 0s appear before the 1s and all the 1s appear before the 2s. This problem is also known as the Dutch national flag problem, named after the Dutch national flag, which has three horizontal bands of red, white, and blue, and it was first introduced by Edsger Dijkstra, a Dutch computer scientist.
The problem arises when an array of integers needs to be partitioned into three groups based on their values This problem has several solutions, including counting the occurrences of 0s, 1s, and 2s and then reconstructing the array in the correct order, using a two-pointer approach, or using a variation of quicksort. The algorithm achieves this by maintaining three-pointers to the array: one for the low end of the 0s, one for the high end of the 2s, and one for the current element being examined. By comparing the current element to the values at the low and high ends, the algorithm moves the elements around until the array is sorted in the desired order.
An example would be an 11-element array with the following values: 0, 1, 1, 2, 2, 1, 0. Our primary task is sorting an array so that all 0s come before all on1s, all 1s before all 2s, and finally, all 2s will fill out the remaining array.
Arr={0 ,2 ,1 ,2, 0, 1, 1 ,2, 0, 2, 1, 0, 1, 0}
Now let’s see the sorted version of the array.
Sorted_Version={0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2}
Methods of Sort Array 0s,1s and 2s
There are two sorting methods used as follows.
1. Brute force approach with the help of double traversal
The brute force approach with double traversal-sort array 0s, 1s, and 2s can be used to sort an array containing only three distinct elements (0s, 1s, and 2s). This approach involves two traversals of the array, and it works by counting the number of 0s, 1s, and 2s in the array in the first traversal and then placing them in the correct order in the second traversal. By using this, we can sort the array in ascending order. In this method, we will see how to write the algorithm for n numbers elements for random numbers as follows.
- Count the number of elements.
- In the second step, we need to scan all the array elements from left to right one by one.
- After scanning, we need to count all 0s from the array list and store them in another.
- In the same way, we need to count all 1s from the array list and store them in another variable.
- Finally, like the above two steps, we need to count all 2s from the array and store them in another.
- If the user enters the elements of an array at runtime, the user must enter the values only in the format of 0s, 1s, and 2; you cannot be sure that the values entered by the user are all in these formats.
- In the above example, we have 5 in 0’s, 5 in 1’s, and 4 in 2’s.
- Now the step, we need to copy all values into the array. Start a loop at the 0th index of an array to copy the values; to begin with, duplicate all quantities of 0’s present in the exhibit while increasing the list esteem. Up to index number 4, all of the 0s will be copied.
- Similarly, copy 1’s and 2’s.
Code:
package com.array;
import java.util.Scanner ;
class Array
{
static void arraysort ( int [] a_xxx , int num )
{
int c_zero = 0 ;
int c_one = 0 ;
int c_two = 0 ;
int i = 0 ;
while ( i < num )
{
if ( a_xxx [ i ] == 0 )
{
c_zero = c_zero + 1 ;
}
if ( a_xxx [ i ] == 1 )
{
c_one = c_one + 1 ;
}
if ( a_xxx [ i ] == 2 )
{
c_two = c_two + 1 ;
}
i = i + 1 ;
}
i = 0 ;
while ( i < c_zero )
{
a_xxx [ i ] = 0 ;
i = i + 1 ;
}
while ( i < c_one + c_zero )
{
a_xxx [ i ] = 1 ;
i = i + 1 ;
}
while ( i < c_two + c_one + c_zero )
{
a_xxx [ i ] = 2 ;
i = i + 1 ;
}
}
public static void main ( String args[] )
{
int num ;
Scanner obj_arrayx = new Scanner ( System.in ) ;
num = obj_arrayx.nextInt() ;
int [] a_xxx = new int[ 100 ] ;
for ( int i = 0 ; i < num ; i++ )
{
a_xxx [ i ] = obj_arrayx.nextInt() ;
}
arraysort( a_xxx , num ) ;
for ( int i = 0 ; i < num ; i++ )
{
System.out.println ( a_xxx [ i ] ) ;
}
}
}Explanation: After execution, we get the below result, as shown in the screenshot.
Output:
2. By using the optimized method of three-way partitioning with single traversal
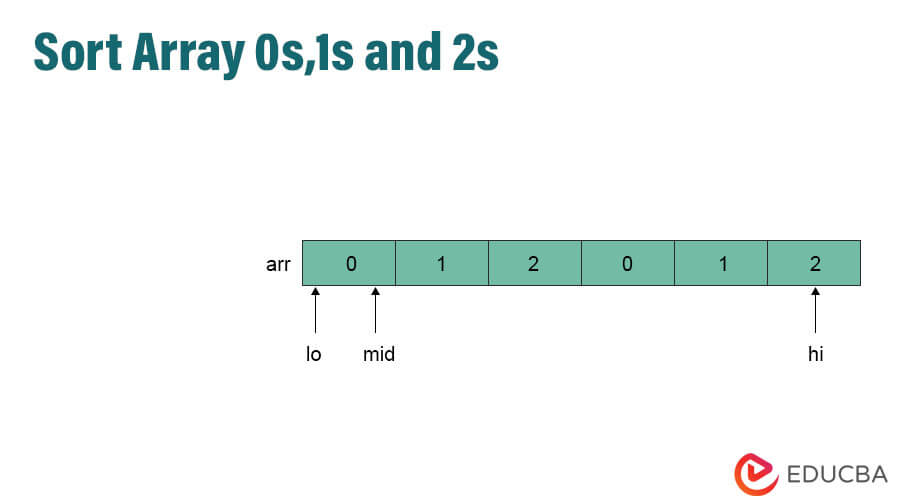
To sort an array of 0s, 1s, and 2s, we can use the optimized method of three-way partitioning with a single traversal. The idea behind this algorithm is to maintain three pointers – low, mid, and high- representing the boundaries of three sub-arrays: 0s, 1s, and 2s.In this method, we can traverse only a single time. Generally, this approach divides us into three different pointers as follows.
Section 1: In this section, we are counting all 0’s that are 0 to low -1.
Section 2: In this section, we count all 1’s that are low to mid -1.
Section 3: In this section, we count all unknown values mid to high-1.
Section 4: In this section, we count all 2’s that are high to n -1.
Now let’s see an algorithm.
- Count the number of elements.
- In the second step, we must divide it into three sections we already discussed.
- At the initial stage, we cannot find how many 0’s, 1’s, and 2’s, so we need to point to two pointers, low =0 and mid =0.
- In the next step, we must execute the loop up to the 13.
- If the mid pointer gets 0, first swap it with the present value at low and increment the pointer by 1, which is low and mid + 1.
- If the mid pointer gets 1, then increment the mid pointer by 1 and continue the loop.
- If the mid pointer gets 2, first swap the present value with a high pointer and increment the high pointer by 1.
- Loop will continue to reach the high pointer and finally get the sorted array.
Code:
package com.array;
import java.util.Scanner ;
class Array
{
static void arraysort ( int [] a_xxx , int num )
{
int arry_low = 0 ;
int arry_mid = 0 ;
int arry_high = num - 1 ;
while ( arry_mid <= arry_high )
{
if ( a_xxx [ arry_mid ] == 0 )
{
int tmp = a_xxx [ arry_mid ] ;
a_xxx [ arry_mid ] = a_xxx [ arry_low ];
a_xxx [ arry_low ] = tmp ;
arry_low = arry_low + 1 ;
arry_mid = arry_mid + 1 ;
}
else if ( a_xxx [ arry_mid ] == 1 )
{
arry_mid = arry_mid + 1 ;
}
else
{
int tmp = a_xxx [ arry_mid ] ;
a_xxx [ arry_mid ] = a_xxx [ arry_high ] ;
a_xxx [ arry_high ] = tmp ;
arry_high = arry_high - 1 ;
}
}
}
public static void main ( String args[] )
{
int num ;
Scanner obj_arrayx = new Scanner ( System.in ) ;
num = obj_arrayx.nextInt() ;
int [] array_sort = new int[ 100 ] ;
for ( int i = 0 ; i < num ; i++ )
{
array_sort[ i ] = obj_arrayx.nextInt() ;
}
arraysort( array_sort , num ) ;
for ( int i = 0 ; i < num ; i++ )
{
System.out.println ( array_sort[ i ] ) ;
}
}
}After execution, we get the below result, as shown in the screenshot.
Output:
Conclusion
In conclusion, Sort Array 0s,1s, and 2s can be solved using various approaches. The Dutch National Flag algorithm involves maintaining three-pointers, low, mid, and high, and partitioning the array into three sections. The time complexity of all these approaches is O(n), where n is the size of the array. We can traverse the array using a third pointer and swap the values as necessary until all the 0s are at the beginning, 1s in the middle, and 2s at the end. This problem is a good exercise for practicing array manipulation and pointer operations in programming.
Recommended Article
We hope that this EDUCBA information on “Sort Array 0s,1s, and 2s” was beneficial to you. You can view EDUCBA’s recommended articles for more information.