SAS Triangle Calculator

Introduction to SAS Triangle Calculator

The SAS triangle calculator helps perform the mathematical operations on the two sides with specified angles. The theorems like the law of cosines, sines, and others are followed to determine the third side so that we can call SAS as Side-Angle-Side triangle for possible combinations. Triangle sides like SSA, angle is included between the two sides, and multiple solutions are followed and used with this scenario.

Key Takeaways

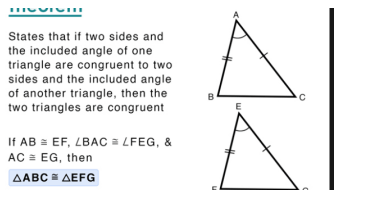
• Mainly two triangles are said to be congruent if the shape and size should be the same.
• We can represent the congruence triangle using the operator ~ and =.
• Then the two sides and angle should be the vertex form from one side of the triangle, equal to the other two corresponding sides.
• Angle formed at the vertex side of another triangle, forming the SAS congruent criteria.
• It can follow the law of cosines and the law of sines theorems.

What is SAS Triangle Calculator?

Triangle calculator is one of the SAS features, and it is most widely used to solve the triangle by the length with two sides and the angle between them. The primary law of cosines can determine the other side, like the third side, with heron’s formula and other trigonometric functions for calculating the triangle area and different property sides. SAS is the theorem that helps to find the area of the triangle across the sides most relevant to the two sides, and it is validated for equal sides, and the angle between the two sides is more equal.

How to Use SAS Triangle?

The area of SAS triangle has performed the calculation with the help of total space, which enclosed it on the 2 dimensional planes, and it recalls the SAS triangle along with the two sides. Wherever the third side is included, the angle between the SAS triangle area occupied the calculation spaces. Additionally, we can call the triangle plane and area of the shape fitted on the square.

Oblique types of triangles do not have the right angles to measure the angle leg and other area parts related to the oblique triangle. In general, two angles, two legs, one side, and one angle with a lot of different combinations for solving the oblique triangles. SAS triangle calculator helps solve the congruent SAS triangle with a combination of the two adjacent sides and the angle between them. So, the combination of the two adjacent sides along with the angle between them for to defining the same time with shape and triangle scale.

To satisfy the SAS triangle condition with two sides, enclose the angle provided with two-line side segments and angles. We can also construct the triangle, which should be constructed with the angle way and segment copy the SAS formula is called and used as the property triangle along with two sides the SAS formula is calculated on the required inputs. Using the law of cosines, the missing triangle side is calculated like the law of sines to perform the two smaller angles on the unknown type. Angle sum followed the triangle rule to find the last angle states that two sides, which included the one triangle congruent for out of two sides. Then it is referred to as the congruent with the same size and shape for corresponding sides and angles should be equal in all areas.

We can create an SAS triangle along with two sides, including the angle mentioned on the congruent side. It’s validated that the triangle sides should be congruent, following the sines and cosines theorem.

How to Solve SAS Triangle Calculator?

To solve the SAS triangle, we can use some trigonometric rules to achieve this with different theorems like the Rule of the sine and the Rule of the cosines.

We can find the rule of the sines and cosines, which states that the corresponding sides are equal angles, and the triangle formula is to be defined and solved in the data iteration.

Above formula is the basic triangle rules that can be used to perform the rule of the cosines which states that the three sides of the triangle for to define in each side of angle.

Here we can perform the SAS triangle operation for assuming the a, b and c sides.

The angle we used to perform the formula is shown below:

The area of the triangle side is calculated using Sine function and whereas the variable called, a and b are the length of the triangle across the two sides. C is the angle included which tends to be the known sides.

Steps to Solve SAS Triangle Calculator

Given below are the steps to solve SAS triangle calculator:

1. Triangles are congruent for the pairs with corresponding sides.

2. A, B, C

3. It should be included both the sides of triangles like (a,c) where as the b is denoted as the <B i.e) angle B.

4. We can use the below formula like:

5. b = a2 + –

6. It can be used to calculate the area of the sides along with the angles.

7. Then we can find out the Angle by using the below formula:

8. A= a

9. The above formula which helps to find out the angle A value.

10. Like that we can calculate the angle C=

Above triangle is the basic diagram to calculate angle of the sides.

We can calculate the Perimeter P= a + b + c. It’s the final output result of the triangle.

SAS Triangle Calculator Rules

Mainly we can calculate the SAS triangle for the two sides and 1 angle.

Here example side1=2 cm, side2= 3 cm, angle=25 degree.

1. First we need to calculate the missing side of the triangle.

res=sqrt(2square + 3square – 2 *2*3*cos(25degree))=1.10

2. After finding the area of the sides we can used the theorems like law of sines for to finding the other side angles.

ß = arcsin(sin(γ) × (b/res))

3. Then we can do the last set of procedure called to complete the triangle calculations that denotes the last side of the angle.

α = 180° – ß – γ

Here the α, ß and res are the variable declaration for performing the SAS triangle calculation.

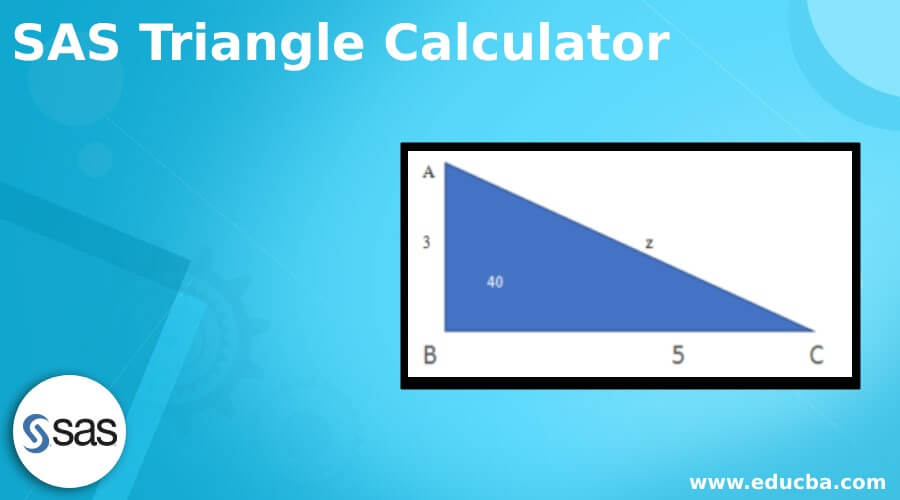
Example of SAS Triangle Calculator

Lets take the below example to solve SAS triangle by using the law of cosine.

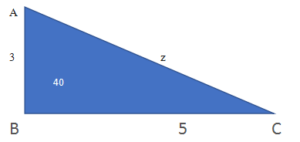
Here AB=3, BC=5 and <ABC=40 degree

We can find the value of the side from AC=? By using law of cosine theorem.

Formula:

=z2=5square+3square-2*3*5 cos40 degree
=25+9-20.008
z=square root(13.99)
z=3.74

Now we can apply the sine theorem rule for calculate the angle C.

Sin C/2=Sin B/z
=Sin 40/3.74
=2*0.74/374
=0.398
<C=sin pow(-1) 0.398=25.37 degree

Triangle is 180 degree.

<A+<B+<C=180
<A+40+25.37=180
<A=180-65.37
<A=2

Output:

The output of the angle <A is 2.

The above example is the basic triangle of to find the triangle side by using the two laws.

FAQ

Given below are the FAQs mentioned:

Q1. What is SAS triangle calculator?

Answer:

It is a Side-Angle-Side to perform the triangle sides operations with the help of sines and cosines theorems.

Q2. What is SAS triangle congruent?

Answer:

It is relevant to the congruence figures for inquiring about the triangle sides even all the pairs and sides are equal.

Q3. Mention the formula for SAS triangle?

Answer:

Area= : 1/2 × bc × sin(A)
Area= : 1/2 × ac × sin(B)
Area= : 1/2 × ab × sin(C)

Conclusion

In SAS triangle the two pairs should be equal and it is made from the congruent which is denoted by the Side-Angle-Side and then the pairs of the two angle sides which are referred is denoted as congruent. By performing the theorems condition the opposite side of the triangle refers to one side of the angle.

Recommended Articles

This is a guide to SAS Triangle Calculator. Here we discuss the introduction, how to use SAS triangle? steps to solve SAS triangle calculator and example. You may also have a look at the following articles to learn more –

1. SASS if() | Examples
2. What is SAS Grid?
3. Create SAS INTCK Function
4. Guide to SAS LAG Function