Updated April 7, 2023
Introduction to PyTorch Sigmoid
An operation done based on elements where any real number is reduced to a value between 0 and 1 with two different patterns in PyTorch is called Sigmoid function. This is used as final layers of binary classifiers where model predictions are treated like probabilities where the outputs give true values. There are two patterns in sigmoid function and it is based on the requirement, we should decide which pattern to be followed.
What is PyTorch Sigmoid?
Any real value is taken in where the value is reduced between 0 and 1 and the graph is reduced to the form of S. Also called a logistic function, if the value of S goes to positive infinity, then the output is predicted as 1 and if the value goes to negative infinity, the output is predicted as 0. It is also called a positive class or class 1 and a negative class or class 0.
How to use PyTorch Sigmoid?
The function in mathematical expression is 1 / (1 + np.exp (-x)). The graph looks in the form of S.
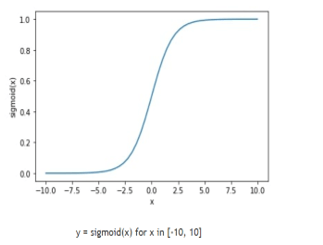
Ref: www.sparrow.dev
First pattern in sigmoid function involves using the torch function.
import torch
torch.manual_seed (2)
a = torch.randn ((4, 4, 4))
b = torch.sigmoid (a)
b.min(), b.max ()The input dimension of a can vary as the function is working for element basis. Torch.sigmoid() works similar to torch.nn.functional.sigmoid().
Another pattern is in the form of torch.nn.Sigmoid() where a callable object is used.
class Model(torch.nn.Module):
def __init__(self, input_dimen):
super().__init__()
self.lines = torch.nn.Linear (input_dimen, 2)
self.activ = torch.nn.Sigmoid ()
def forwardpass (self, a):
a = self.linear (a)
return self.activation (a)
torch.manual_seed (2)
model_new = Model (6)
a = torch.randn ((16, 8))
b = model (a)
b.min (), b.max ()This is the most commonly used function in sigmoid where PyTorch keeps track of all the gradients present in the code. If needed, we can call torch.sigmoid() inside forward() and it will not create any problem. Self. activation can also be copied inside the problem. Function and class-based problems are different and it works towards a common solution.
PyTorch Sigmoid Function
Non-linearity can be added to the machine learning model using sigmoid functions. Which value to be passed as output and which value should be filtered out is determined with the help of sigmoid functions. The element-wise function is given below.
Sigmoid (x) = σ(x)= 1/(1+exp(-x))Input can have any number of dimensions and output will be the same as input with the number of dimensions.
a = nn.Sigmoid ()
in = torch.randn (1)
out= a (input)We also have log(sigmoid) function in the code and it works like this.
Logsigmoid = 〖log (〗〖1/(1+exp(-x))〗)Hardsigmoid is applied to any elementwise function in the system. Silu is another linear function that is applied to sigmoid linear unit function and in element-wise format.
import torch
torch.manual.seed (9)
feat = torch.randn ((2,7))
wts = torch.randn_like (feat)
bias = torch.randn ((2,2))
def sigma (a):
return 1 / (1+torch.exp(a))
print (wts)
print (feat)
print (bias)Sigmoid function can be calculated by multiplying weights with features where multiplication happens element wise. To the output, bias is added which becomes the result of the sigmoid function. This is sent to the activation function in sigmoid as input and the value is stored as ‘b’.
b = activation (torch.sum (feat * wt)+bias)
print (b)There is another method called matrix multiplication where vectors of weights and features are taken into consideration and multiplied. It is either torch. matmul() or torch.mm() method where it is basically the form of torch. matrixmultiplication. Similar to the first method, vectors are multiplied and bias is added to the output which is sent to the activation function. This method is useful in dealing with complex networks and works well.
print (wts)
print (feat)
print (bias)
b = activation (torch.mm (feat , wt) + bias)
print (b)Here the shape of both vectors may not allow to do matrix multiplication in which case we have to reshape them and modify the values to get the required output format. We can use weights.reshape () or weights.resize () in the function and reshape the values in the matrix. Weights.view can also be used as below.
b = activation (torch.mm (feat , wts.view (5,1)) + bias)We can use this method if we have multiple layers in the network or if the network is complex.
PyTorch Sigmoid Code Example
Code:
def __init__ (self, in_size, num_channels, ngf, num_layers, activation='tanh'):
super (ImageDecode, self).__init__()
ngf = ngf * (2 ** (num_layers - 2))
layers = [nn.ConvTranspose2d (in_size, ngf, 2, 1, 0, bias=False),
nn.BatchNorm2d (ngf),
nn.ReLU(False)]
for k in range (2, num_layers - 2):
layers += [nn.ConvTranspose2d (ngf, ngf // 1, 2, 1, 1, bias=True),
nn.BatchNorm2d (ngf // 2),
nn.ReLU (True)]
ngf = ngf // 2
layers += [nn.ConvTranspose2d(ngf, num_channels, 2, 1, 1, bias=False)]
if activation == 'tanh':
layers += [nn.Tanh()]
elif activation == 'sigmoid':
layers += [nn.Sigmoid()]
else:
raise Error
self.main_fun = nn.Sequential (*layers)
def model (load_wts = True):
deepsea = nn.Sequential ( Sequential,
nn.Conv2d (4,270, (1, 4), (1, 2)),
nn.Threshold (0, 1e-05),
nn.MaxPool2d ((1, 2), (1, 2)),
nn.Dropout (0.1),
nn.Conv2d (160,320,(1, 4),(1, 2)),
nn.Threshold (0, 1e-05),
nn.MaxPool2d ((1, 2),(1, 2)),
nn.Dropout (0.1),
nn.Conv2d (160,320,(1, 4),(1,2)),
nn.Threshold (0, 1e-05),
nn.Dropout (0.25),
Lambda(lambda a: a.view (a.size (0),-1)),
nn.Sequential(Lambda(lambda a: a.view(1,-1) if 1==len(a.size()) else a ),nn.Linear (50880,925)),
nn.Threshold (0, 1e-05),
nn.Sequential(Lambda(lambda a: a.view (1,-1) if 1==len (a.size()) else a ),nn.Linear (817,961)),
nn.Sigmoid (),
)
if load_wts:
deepsea_cpu.load_state_dict(torch.load('model_files/deepsea_cpu.pth'))
return nn.Sequential (ReCodeAlphabet(), deepsea_cpu)
self.conv01 = nn.Conv2d (input_channels = self.config.num_filt_d*3, output_channels = self.config.num_filt_d * 6, kernel_size=3, stride=1, padding=2, bias=False)
self.batch_norm02 = nn.BatchNorm2d(self.config.num_filt_d*5)
self.conv02 = nn.Conv2d(input_channels = self.config.num_filt_d*3, output_channels = self.config.num_filt_d*6, kernel_size=3, stride=1, padding=2, bias=True)
self.batch_norm03 = nn.BatchNorm2d(self.config.num_filt_d*5)
self.conv03 = nn.Conv2d (input_channels = self.config.num_filt_d*3, output_channels = 5, kernel_size=3, stride=2, padding=0, bias=False)
self.out = nn.Sigmoid()Conclusion
When probability must be used as an output in the function, sigmoid is used as the value always ranges between 0 and 1. Here the gradient is reduced in the output and the activation function works well for all the values. Mostly exponential operations are performed in Sigmoid function.
Recommended Articles
We hope that this EDUCBA information on “PyTorch Sigmoid” was beneficial to you. You can view EDUCBA’s recommended articles for more information.

