Python Z Test

Introduction to Python Z Test

The following article provides an outline for Python Z Test. In the vast field of statistics, the process of hypothesis testing plays a very major role. The hypothesis testing helps to make a decision on a statistics assumption. When a hypothesis is formed, the hypothesis testing is used to confirm how close the assumption is to reality. This is the key characteristics of hypothesis-based testing. In hypothesis testing, the Z test is a method or a type of testing used.

The Z test involves determining the P-value and then verifying how close the determined P value is close to the significance value which is considered. Usually, the significance value is around 0.05. The P value stands for the representation of the probability value identified. The probability value mentions on how much possible the determined assumption is a null hypothesis or an alternative hypothesis. So based on the P value determined, the reality of the hypothesis assumption is validated. This is the key process of the Z test.

Z Test Syntax

Given below is the syntax mentioned:

statsmodels.stats.weightstats.ztest(x1, x2=None, value=0, alternative='two-sided', usevar='pooled', ddof=1.0)

• The Z test model can take in two independent samples for processing and determining the p value. In the above syntax, the x1 will be the first independent sample used. Therefore, the x1 needs to be keyed in the form of an array in one dimensional or two-dimensional format.
• In the above syntax, the x2 will be the second independent sample used. The x2 needs to be keyed in the form of an array in one dimensional or two-dimensional format.
• The value will hold the mean of X1, which forms the alternative hypothesis. When more than one independent variable is used, this value will be the mean of the difference between X1 and X2.
• The user holds the value pooled, which means the standard deviation of the samples is the same.
• H1 refers to the alternative hypothesis.
• ddof is used for mean estimate calculation.

When to Perform Z Test in Python?

• First, the size of the sample used determines when the Z test needs to be performed. This means whenever the size of the sample is larger than 30 records, then the Z test is preferred. So the sample size plays a key in Z test determination. When the number of sample records involved is lesser than 30, then the t-test is preferred over the Z test.
• Every datapoint involved needs to be independent between each other. This means both the datapoints involved in the Z test needs to be self-governing, then the data used must be suitable for the Z test. This is another key functionality for considering the Z test in python.
• The normal distribution of the data is expected. Especially for smaller sample sizes, this needs to be strictly followed. The normal distribution of the sample sizes is a key factor for this Z test selection. When the sample size is greater than 30 records, it can be considered without having the normal distribution in place.
• The method of sampling is another key factor used. This determines how precise the hypothesis is calculated. Here we need to ensure the data selected in the sample is well distributed and randomly selected. So from a large set of population, it is necessary to ensure the data is well shuffled and selected from this large set so that all aspects of the population can be covered in the sample set.

Examples of Python Z Test

Given below are the examples of the Python Z Test:

Data Used ( BP.csv ):

patient_name	patient_ sex	patient_agegrp	patient_bp_before	patient_bp_after
1	Male	30-45	142	153
2	Male	30-45	163	170
3	Male	30-45	143	168
4	Male	30-45	153	142
5	Male	30-45	146	141
6	Male	30-45	150	147
7	Male	30-45	158	133
8	Male	30-45	153	141
9	Male	30-45	153	131
10	Male	30-45	158	125
11	Male	30-45	169	164
12	Male	30-45	173	159
13	Male	30-45	165	135
14	Male	30-45	145	159
15	Male	30-45	133	153
16	Male	30-45	152	126
17	Male	30-45	141	162
18	Male	30-45	176	134
19	Male	30-45	143	136
20	Male	30-45	162	150
21	Male	46-59	149	168
22	Male	46-59	156	155
23	Male	46-59	151	136
24	Male	46-59	159	132
25	Male	46-59	164	160
26	Male	46-59	154	160
27	Male	46-59	152	136
28	Male	46-59	142	183
29	Male	46-59	162	152
30	Male	46-59	155	162
31	Male	46-59	175	151
32	Male	46-59	184	139
33	Male	46-59	167	175
34	Male	46-59	148	184

Example #1

Code:

import pandas as pd
from statsmodels.stats import weightstats as stests
dataframe = pd.read_csv(r"C:\Users\ANAND\Desktop\BP.csv")
dataframe[['patient_bp_before','patient_bp_after']].describe()
ztest ,propability_value = stests.ztest(dataframe['patient_bp_before'], x2=None, value=146)
print(float(propability_value))
if propability_value<0.05:
    print("Null hyphothesis rejected , Alternative hyphothesis accepted")
else:
    print("Null hyphothesis accepted , Alternative hyphothesis rejected")

Output:

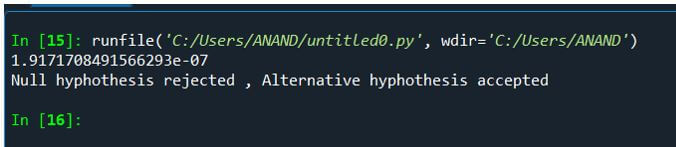
Explanation:

• In this first example, the following assumptions are made.
• Alternative Hypothesis: The average BP of all the patients ranges around 146 in before.
• Null Hypothesis: The average BP of all the patients does not provide a range in the given value of the mean.
• When the probability value is determined, and the hypothesis is evaluated, the probability values lie somewhere around -1.91, which is lesser than the 0.05 significance level; hence, this is considered an Alternative hypothesis. Hence the assumption is successful.

Example #2

Code:

# The Mean value is alone manipulated as 78
ztest ,propability_value = stests.ztest(dataframe['patient_bp_before'], x2=None, value=146)

Output:

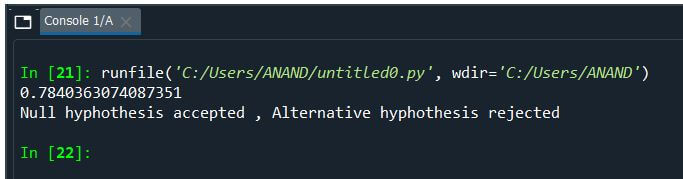
Explanation:

• In this second example, the following assumptions are made.
• Alternative Hypothesis: The average BP of all the patients ranges around 78 in before.
  Null Hypothesis: The average BP of all the patients does not provide a range in the given value of the mean.
• When the probability value is determined, and the hypothesis is evaluated, the probability values lie somewhere around +0.78, which is greater than the 0.05 significance level; hence, this is considered a Null hypothesis. Hence the assumption has failed.

Conclusion

Among the different methods for hypothesis testing, the Z test is one of the most stable methods used. This method offers a lot of flexibility in determining the p value involved and identifying the type of hypothesis happening. So, the presence of the Null hypothesis or alternative hypothesis can be flexibly calculated.

Recommended Articles

This is a guide to Python Z Test. Here we discuss the introduction, when to perform the z test in python and examples for better understanding. You may also have a look at the following articles to learn more –

1. Shell sort in Python
2. Insertion sort in Python
3. Flask in Python
4. Python List extend