Updated August 30, 2023
Percentile Rank Formula (Table of Contents)
- Percentile Rank Formula
- Percentile Rank Calculator
- Percentile Rank Formula in Excel (With Excel Template)
Percentile Rank Formula
Percentile Rank is a common term in statistics that is derived from Percentile. Percentile (also known as centile) is the percentage of scores ranging from 0 to 100 that is less than or equal to the given set of distributions.
Percentiles divide any distribution into 100 equal parts. The process primarily utilizes this method to interpret scores from different tests with varying ranges. The Percentile Rank (PR) is determined by considering the total number of ranks as well as the number of ranks below and above the percentile. The formula is a simple percentile to percentage converter.
A formula for Percentile Rank is as below:
To identify percentile rank (PR) of score x, out of N (where x is included).
Where,
- M = Number of Ranks below x
- R = Number of Ranks equals x
- Y = Total Number of Ranks
To identify percentile rank (Per Rank) of score x, out of Y (where x is not included).
Where,
- M = Number of Ranks at x
- Y = Total number of Ranks
Percentile is mainly applied to the data set of scores where ranking needs to be identified. In addition, every 25th percentile is known as one quartile. Out of 100, the 25th percentile is known as the 1st quartile. The 50th percentile is the 2nd quartile or median, and the 75th percentile is the 3rd quartile. The difference between the 3rd and 1st quartile is called an Interquartile range.
Examples of Percentile Rank Formula
Let’s take an example to understand the calculation of Percentile Rank and how to use this percentile to percentage converter.
Example #1
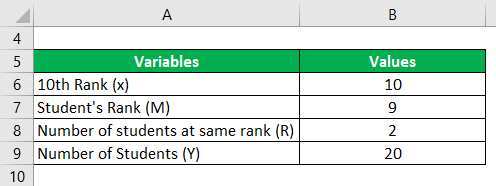
Assume that a class has 20 students. All are taking the NEET exam to further their education. Babu and Sudha are two of the 20 students, and both are ranked 10th. Calculate Babu’s Percentile Rank.
Solution:
- In this case, the total number of ranks will be the same as the total number of students. So Y will be 20.
- Percentile rank needs to be calculated for Babu, who is at 10th rank. Hence x will be 10.
- We need to identify the count of the same 10th rank. In this case, it will be Babu and Sudha. So R will be 2.
- We need to count the ranks that are less than 10, which will be considered as M. Hence M will be 9.
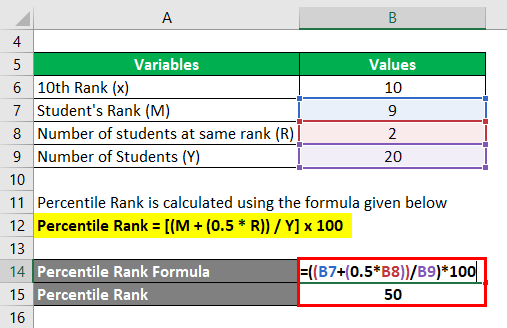
Percentile Rank = [(M + (0.5 * R)) / Y] x 100
- Percentile Rank = [(9 + (0.5 * 2)) / 20] * 100
- Percentile Rank = [(9+1) / 20] * 100
- Percentile Rank = [10 / 20] * 100
- Percentile Rank = 0.5 * 100
- Percentile Rank = 50%
Hence the percentile rank for Babu will be 50%. Babu is standing at the 50th percentile in his class!!
Example #2
10 students attended the Aptitude test in an organization. The scores of the students are 5, 9, 4, 12, and 7. Identify the percentile rank for score 9.
Solution:
- Step 1: Arrange the score data set in ascending order: 4, 5, 7, 9, 12.
- Step 2: Add ranking for the ordered score:
| Score |
4 |
5 |
7 |
9 |
12 |
| Ranking |
1 |
2 |
3 |
4 |
5 |
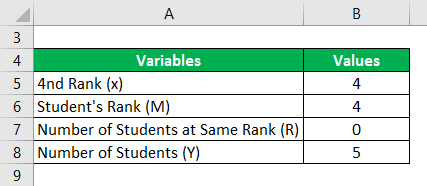
- In this case, the total number of ranks will be the same as the total number of students. So Y will be 5.
- Percentile rank needs to be calculated for score 9, the 4th rank. Hence x will be 4.
- Count the ranks at 4, which will be considered “M“. Hence M will be 4.
- We need to identify the count of the same 10th rank. In this case, it will be 0. So we will be using the second formula.
Percentile Rank = [M / Y] x 100
- Percentile Rank = [4/5] *100
- Percentile Rank = 0.8 * 100
- Percentile Rank = 80%
This concludes score 9 is higher than 80% of the scores.
Explanation
Below is the step-by-step approach for attaining the Percentile Rank value.
Step 1: Note down the value of the scores in ascending order (lowest to highest), along with ranking in a tabular format. Count the number of scores or the last rank, which will be considered “Y – Total number of ranks”.
Step 2: Identify the score x for which the percentile needs to be calculated.
Step 3: Identify if it is the same score as x. If yes, count the same score as “R”.
Step 4: Count the scores that are less than x, which will be considered as “M”. Thus, the formula is,
Percentile Rank = [(M + (0.5 * R)) / Y] x 100
Step 5: If the value of “R” is zero in step 3, then the formula is,
Percentile Rank % = [M / Y] x 100 %
Relevance and Uses
There is no universally defined formula for Percentile and Percentile Rank. However, people predominantly use these measures to rank examinations such as NEET, GRE, SAT, LSAT, etc. These measures commonly help identify a method for interpreting one’s position in a standard dataset. In the current digital world, this is also used to interpret medical details such as percentile laparoscopy failures during operations and in data science as well!!
Percentile Rank Formula Calculator
You can use the following Percentile Rank Calculator
| M | |
| R | |
| Y | |
| Percentile Rank Formula | |
| Percentile Rank Formula | = |
|
||||||||
| = |
|
Percentile Rank Formula in Excel (With Excel Template)
Here we will see an example of the Percentile Rank formula in Excel. It is very easy and simple.
In Excel, some values are in Example: 1 and Example: 2 tabs. Example 1 can be used for Formula: 1, and example: 2 can be used for Formula: 2. These two are based on two different formulae, as mentioned above, and can be used based on the scenarios. Please follow the below steps to use percentile to percentage converter.
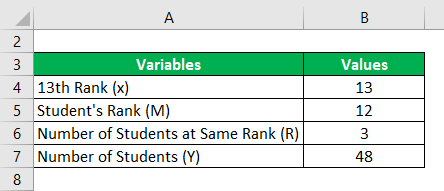
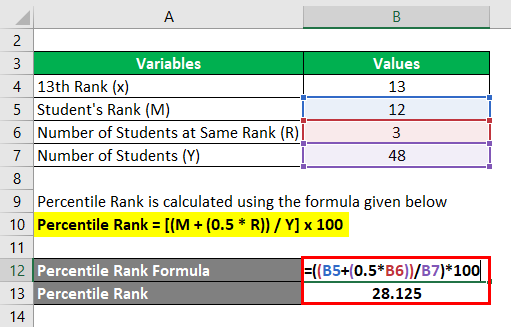
For Sample A
Percentile Rank = [(M + (0.5 * R)) / Y] x 100
- Percentile Rank = [(12 + (0.5 * 3)) / 48] * 100
- Percentile Rank = [(12+1.5) / 48] * 100
- Percentile Rank = [13.5 / 48] * 100
- Percentile Rank = 0.28125 * 100
- Percentile Rank = 28.125%
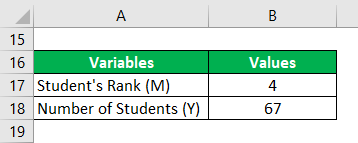
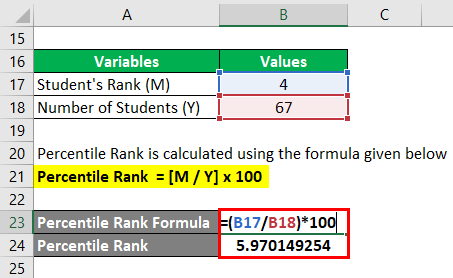
For Sample B
Percentile Rank = [M / Y] x 100
- Percentile Rank = [4/67] *100
- Percentile Rank = 0.05970149254 * 100
- Percentile Rank = 5.970149254%
Recommended Articles
This has been a guide to Percentile Rank Formula. Here we have discussed how to calculate Percentile Rank along with practical examples. We have also provided a Percentile Rank calculator with a downloadable Excel template. You may also look at the following articles to learn more –