Updated April 18, 2023
Introduction to NumPy correlation
Numpy.correlation in Python is excited by the application of the correlate * () function. It is used in the Python coding language that Enables the cross-correlation ship between two unique One dimension of single dimension arrays containing a sequence of data set. This function is enabled to perform computation upon the correlation as it is generally defined in the process of signal enhancement and evaluation.
Syntax and Parameters of numpy.correlate* ()
Following is the syntax which used to utilize the numpy.correlate*() while writing codes in the Python programming language:
numpy*.* correlate* (* a1, v1, mode='valid', * old* _* behavior* =* False)The following is the parameters used for the numpy.correlate() function written in the Python programming language:
| Parameter | Description of the Parameter |
| a1 single dimensioned array or sequence of array_like
They represent the input variable; all the single-dimensional array is that have been entered into the system by the user. They contain a sequence of data which can be random or having a pattern mode* ** ** ** ** *{* * ‘valid’, * * ‘same’, * * ‘full’* *},* * optional* ** ** * This refers to the conversation that is expected in the docstring. It is an optional variable that is used in the parameter while using the function. It must be noted that the parameter has its default value set as valid. Unlike the similar function of convolving, which is a default set at ‘full.’ old_behavior : bool* ** ** * In case the parameter turns out to be true, it utilizes the previously existing behaviour from the numeric, * * (correlation* * (a1,v1) =* *= * *correlation* * (v1,a1), and then further conjugate is not considered for utilisation on complex arrays. Increase the value set for the parameter is false; it then utilizes the pre-defined conventional signal processing. |
|
| Returns | Out: ndarray, optional* ** *
The parameter enables the program to show the exact destination where the correlation executed resultant array has to be placed. This parameter is not an unnecessary addition and can be skipped while writing the command. |
How does NumPy correlation work?
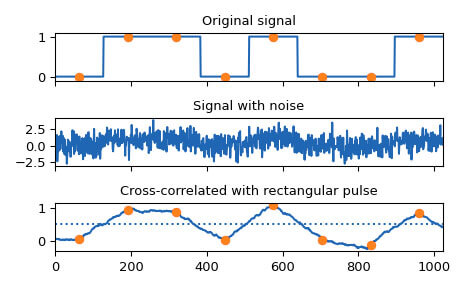
Fig: The diagrammatic representation of the cross-sectional correlation between the original signal which is produced any noise which is capture with the signals to finally provide a defined rectangular pulse
In audio signal processing, the cross-correlation defines a standardized measure to indicate the similarities observed between two series of data sets that act as a function in terms of the displacement in terms of contrasting relativity from one another. This kind of phenomenon is also popularly known as the sliding inner product of the sliding dot product. It is generally utilized for the purpose of searching for exceptionally long on lengthy signals for the shorter duration, which is termed as a feature. It has a major application to be seen in recognising patterns detected by sound waves, analysis of single particle, the process of averaging, in the neurophysiology, decrypting, and electron tomography process.
In order to analyze how the function correlation works, the first thing that has to be done is to see the availability of the function and how all or some of them can be utilized. There are various kinds of calculations that have been categorized in terms of correlation. The correlation of several time series, which are inclusive of a comparatively left copy of the sequence itself, is termed as autocorrelation. While on the contrary, cross-correlation ship is suggested to be a kind of correlation series of elements of sequences which are consisting of the payment, which may or may not be inclusive of the lags.
Examples of NumPy correlation
An example displaying the used of NumPy.correlate() in Python to perform correlation:
Example #1
Code:
# Python program explaining the use of NumPy.correlate () function import numpy as geek1
# Python program explaining
# numpy.correlate() function
# importing numpy as geek
import numpy as geek1
print("Input the value for the array that has to given")
a1 = [20, 50, 70]
v1 = [0, 10, 0.50]
print("The Output with the application of the numpy's correlation function is: ")
gfg1 = geek1.correlate(a1, v1, "same")
print(gfg1)Output:
Example #2
Code:
# Python program explaining the use of NumPy.correlate () function import numpy as geek2
# Python program explaining
# numpy.correlate() function
# importing numpy as geek2
import numpy as geek2
print("Input the value for the array that has to given: ")
a2 = [200, 500, 700]
v2 = [0, 100, 50]
output = geek2.correlate(a2, v2)
print("The Output with the application of the numpy's correlation function is: ")
print(output)Output:
Conclusion
The NumPy. concatenate() function is essential in use, as the cross-correlation defines a standardized measure to indicate the similarities observed between two series of data sets that act as a function in terms of the displacement in terms of contrasting relativity from one another. This kind of phenomenon is also popularly known as the sliding inner product of the sliding dot product. It is generally utilized for the purpose of searching for exceptionally long on lengthy signals for the shorter duration, which is termed as a feature. It has a major application to be seen in recognising patterns detected by sound waves, analysis of single particle, the process of averaging, in the neurophysiology, decrypting, and electron tomography process.
Recommended Articles
This is a guide to the NumPy correlation. Here we discuss How does NumPy correlation work and Examples along with the codes and outputs. You may also have a look at the following articles to learn more –