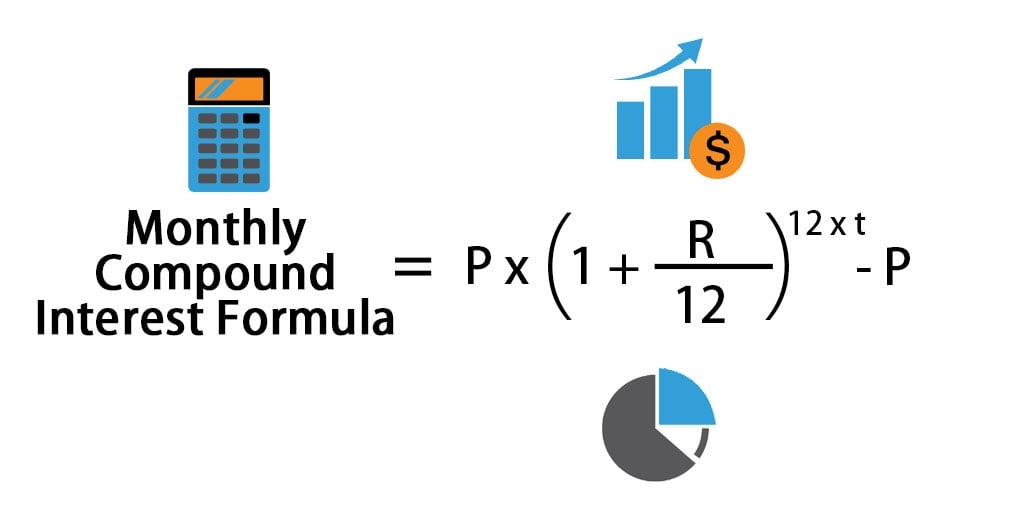Updated October 5, 2023
Table of Contents
What Does the Monthly Compound Interest Formula Do?
When you borrow or lend a certain amount of money for a specific duration, you pay or receive an extra amount apart from the borrowed amount. This extra amount is called interest, and the Monthly Compound Interest Formula calculates this interest that you pay/earn per month on the initial sum of money (the principal) over time.
In simple interest, you find the loan’s interest amount for the year and add it to the loan amount to get the final amount you must pay. However, with monthly compound interest, we take a different approach:
- We find the interest for month 1 based on the initial principal amount (P).
- Then, we add 1st month’s interest to the initial principal amount to find the new principal amount, let’s call it P1.
- Next, we find the interest amount for month 2 based on the new principal amount (P1).
- Again, we add the calculated interest to P1 to find P2
- We keep repeating this process for each month.
So, if you notice, the interest for every new month not only includes interest on the initial amount but also on the interest that we already added to the previous months’ principal amounts.
Formula
Where,
- P: Principal Amount
- r: Annual Interest Rate
- t: Time in Years
Examples of Monthly Compound Interest Formula (With Excel Template)
Let’s take an example to understand the calculation of Monthly Compound Interest in a better manner.
Example #1
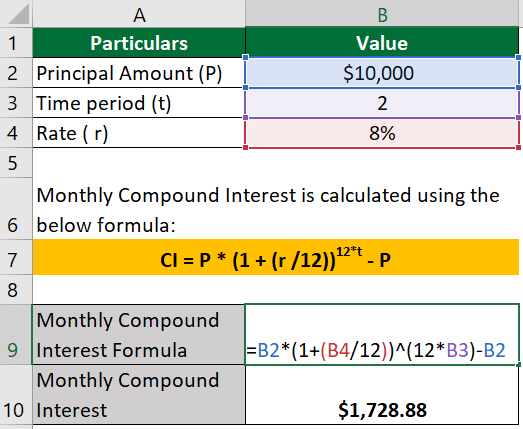
Samuel borrowed $10,000 at an annual interest rate of 8%. What monthly compounded interest will he have to pay over 2 years?
Solution:
The formula to calculate Monthly Compound Interest is as follows:
CI = P x (1 + (r /12))12xt – P
= $10,000x(1 + (8%/12))(12×2) – $10,000 = $11,728.88 – $10,000
= $1,728.88
So, the monthly compounded interest Samuel would incur over a period of 2 years is approximately $1,728.88.
Example #2
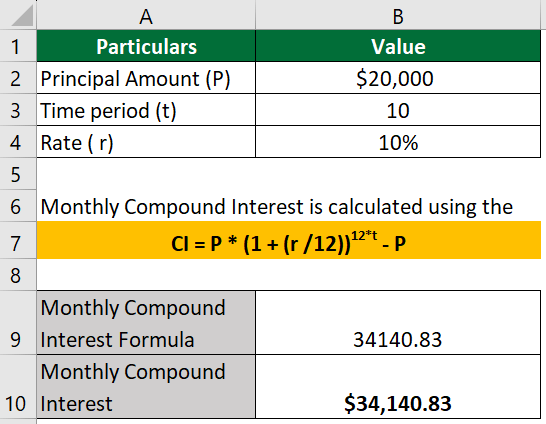
If you invested a principal amount of $20,000 at an annual interest rate of 10%, what will be the monthly compounded interest you will earn in 10 years?
Solution:
The formula to calculate Monthly Compound Interest is:
CI = P x (1 + (r /12))12xt – P
= $20,000 (1 + 10%/12))(12×10) – $20,000 = $54,140.83 – $20,000
= $34,140.83
So, the monthly compounded interest earned over 10 years is approximately $34,140.83.
Example #3
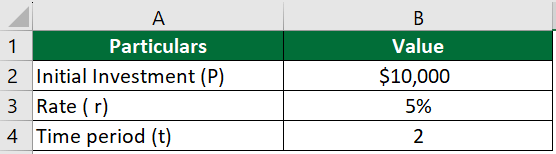
Suppose you have $10,000 (P) that you invest in a savings account with an annual interest rate of 5% (r), and you plan to leave the money in the account for 2 years (t). Calculate the monthly compound interest.
Given:
Solution:
CI = P x (1 + (r /12))12xt – P
= $10,000 x (1 + (5%/12))12×2 – $10,000 = $11,049.41 – $10,000
= $1,049.41
How to Calculate Monthly Compound Interest?
If you want to calculate monthly compound interest manually, here’s a step-by-step guide:
- Convert the annual interest rate (r) from a percentage to decimal by dividing it by 100. For example, if the annual interest rate is 5%, r = 0.05.
- Divide the annual interest rate (r) by 12 to get the monthly interest rate: =(r/12)
- Add 1 to the result you get after dividing r by 12: =1 + (r/12)
- Multiply the number of years (t) by 12 to convert it to the number of months: = t x 12
- Raise the value of (1 + (r/12)) to the power of the calculated number of months (t x12): =(1 + (r/12)) ^ (tx12)
- Multiply the principal amount with the final result of Step 5:
= P x (1 + (r/12)) ^ (tx12) - Subtract the principal amount from the final result of Step 6:
= P x (1 + (r/12)) ^ (tx12) – P
Calculator
You can use the following Monthly Compound Interest Formula Calculator.
| P | |
| r | |
| t | |
| Monthly Compound Interest Formula | |
| Monthly Compound Interest Formula = | P x [(1 +r/12)12xt - P] |
| = | 0 x [(1 +0/12)12x0- 0] = 0 |
Recommended Articles
This article on Monthly Compound Interest Formula guides you on how you can calculate monthly compound interest. You can also refer to the following similar articles: