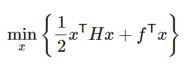Updated March 6, 2023
Introduction to Matlab quadprog
The following article provides an outline for Matlab quadprog. The quadprog or quadratic programming is used to minimize or maximize the input objective function subjected to various constraints. Quadratic programming is used in mathematics to find a vector ‘x’, minimising a quadratic function defined as minx{1/2 * x^T *Hx + f^T * x}.
Or
The following constraints are applied to the quadratic function:
- Ax ≤ b (inequality constraint)
- Ax = b (equality constraint)
- LowerBound ≤ x ≤ UpperBound (bound constraint)
In the real world, quadratic programming is used to solve problems, including power generation, portfolio management, design optimization, etc.
Syntax of quadprog Function
Given below is the syntax mentioned:
x = quadprog (H, f, A, b)
Explanation:
- x = quadprog (H, f, A, b) is used to minimize the quadratic function 1/2 * x^T * Hx + f^T * x subjected to the constraints A*x ≤ b.
Note that the input matrix ‘H’ must be a positive definite for quadratic programming if we need our problem to give a finite value minimum.
Examples of Matlab quadprog
Given below are the examples of Matlab quadprog:
Example #1
This example will use the quadprog function to minimize the objective function “1/2 * x^T *Hx + f^T * x”. For this example, we will use a 3 x 3 input matrix.
Below are the steps to be followed:
- Initialize a 2 x 2 input matrix ‘H’ for the input objective function.
- Initialize the vector ‘f’ for the input objective function.
- Declare the required constraints.
- Use the quadprog function to minimize the objective function.
Code:
H = [1 3; -1 2] [Initializing the matrix ‘H’ for the input objective function]
f = [-1; 3] [Initializing the vector ‘f’ for the input objective function]
A = [1 0; -1 -2; 0 1];
b = [2; 2; 3];
[Declaring the constraints]
[FinalPoint, FunctionVal, ExitFlag, Op, L] = quadprog(H, f, A, b);
[Using the quadprog function to get the required values for the objective function]
FinalPoint, FunctionVal, ExitFlag
Input:
Output:
Output 1:
Output 2:
As we can see in the output, our objective function is now minimized under constraints defined by us. Also, we have obtained the Exit Flag as 1, which implies we have obtained a local minimum for our objective function.
Example #2
This example will use the quadprog function to minimize the objective function “1/2 * x^T *Hx + f^T * x”. For this example, we will use a 3 x 3 input matrix.
Below are the steps to be followed:
- Initialize a 3 x 3 input matrix ‘H’ for the input objective function.
- Initialize the vector ‘f’ for the input objective function.
- Declare the required constraints.
- Use the quadprog function to minimize the objective function.
Code:
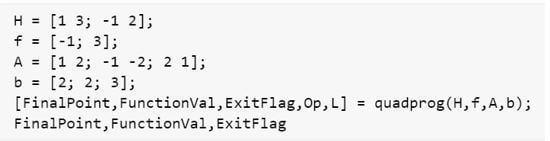
H = [1 1 0; 1 1 1; 1 0 1] [Initializing the matrix ‘H’ for the input objective function]
f = [-1; 1; 1] [Initializing the vector ‘f’ for the input objective function]
A = [1 1 2; 1 -2 1; 1 2 1];
b = [1; -1; 1];
[Declaring the constraints]
[FinalPoint, FunctionVal, ExitFlag, Op, L] = quadprog(H, f, A, b);
[Using the quadprog function to get the required values for the objective function]
Input:
Output:
Output 1:
Output 2:
As we can see in the output, our objective function is now minimized under constraints defined by us. Also, we have obtained the Exit Flag as 1, which implies we have obtained a local minimum for our objective function.
In the above 2 examples, the input matrix ‘H’ was convex, i.e. positive definite, and so we got a local minimum. If our matrix is not convex, we will not get a local minimum.
Example #3
This example will use the quadprog function to minimize the objective function “1/2 * x^T *Hx + f^T * x”. For this example, we will use a 3 x 3 input matrix.
Below are the steps to be followed:
- Initialize a 3 x 3 input matrix ‘H’ for the input objective function, such that the matrix is not positive definite.
- Initialize the vector ‘f’ for the input objective function.
- Declare the required constraints.
- Use the quadprog function to minimize the objective function.
Code:
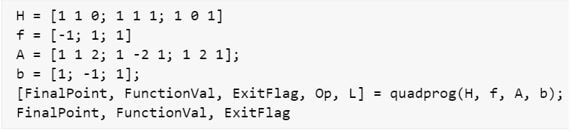
H = [1 2 0; 3 1 2; -1 0 1] [Initializing the matrix ‘H’ for the input objective function]
f = [-1; 1; 1] [Initializing the vector ‘f’ for the input objective function]
A = [1 1 2; 1 -2 1; 1 2 1];
b = [1; -1; 1];
[Declaring the constraints]
[FinalPoint, FunctionVal, ExitFlag, Op, L] = quadprog(H, f, A, b);
[Using the quadprog function to get the required values for the objective function]
Input:
Output:
Output 1:
Output 2:
As we can see in the output, the Exit Flag is-6, which implies we have not obtained any local minimum for our objective function.
Conclusion
We use quadprog function to find the local minimum of our objective function, which is subjected to some constraints. We will get local minimum only if the matrix ‘H’ is positive definite in nature.
Recommended Articles
This is a guide to Matlab quadprog. Here we discuss the introduction and examples of Matlab quadprog for better understanding. You may also have a look at the following articles to learn more –