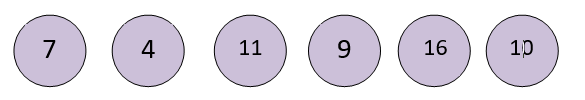Updated March 8, 2023
Introduction to Insertion Sort Recursive
Insertion Sort is an easy and one of the efficient sorting techniques that work the same way as you sort a pack of cards in your hand. This algorithm technique is based on a deck of cards in which you sort the card according to another card. Most of the players prefer sorting in ascending order, and it works the same way in this sorting technique as well.
A number is compared to another number then shifted to the correct place where it needs to be, and all the other elements are sorted in the same way. Since it uses nested loops for sorting elements, this technique cannot sort numbers quickly.
Concept of Insertion Sort
By using Insertion sort, the array is divided into two parts that are, an unsorted array and a sorted one. This sorting technique is performed by moving every element in the correct position by comparing it with the other. One element is selected as a key element and using that element, it is compared with other elements in the array and then sent to the left side of the array when the particular element is smaller than the key element and it will remain on the right side when the selected element is greater than the key element. This process will recursively happen until all the elements in the array are sorted.
Insertion Sort Algorithm
To sort an array of size n, we need to follow the following algorithm.
Step 1: Define a function that will sort the array passed to it.
Step 2: Call the function recursively.
Step 3: Sort the first n-1 elements of the array by recursively calling it.
Step 4: Take the nth element of the array and insert it into the sorted n-1 elements at the appropriate position.
Step 5: Print the sorted array.
Source Code:
#Insertion Sort Recursive
# Performing insertion Sort recursively
def insertionSortRecursive(arr , n):
# base case
if n <= 1:
return
# Sorting the elements in the array
insertionSortRecursive(arr , n - 1)
# Assigning the element to last variable
last = arr[n - 1]
j = n - 2
# moving ahead
while (j >= 0 and arr[j] > last):
arr[j + 1] = arr[j]
j = j - 1
arr[j + 1] = last
# The main part of assigning the array and calling the function
elements = [1 , 5 , 3 , 4 , 8 , 6 , 3 , 4 , 5]
n = len(elements)
insertionSortRecursive(elements ,n)
print()
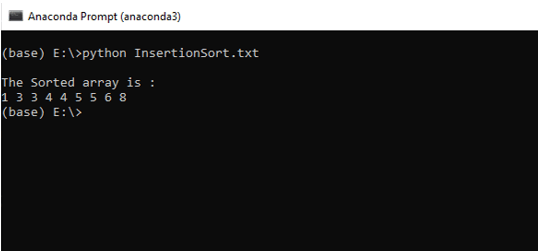
print("The Sorted array is : ")
for i in range(n):
print(elements[i], end = " ")
Output:
Example
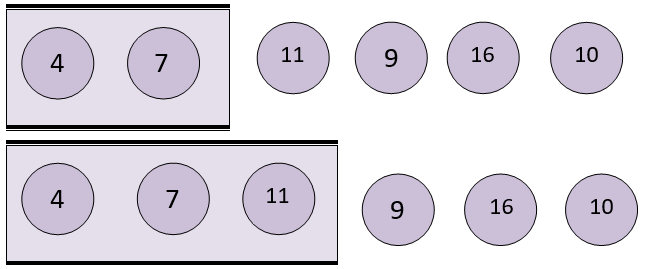
Let us look at an example of how the above code works. Take an unsorted array as shown below.
The array consists of elements whose length will be 6 and the index starts from 0 to 5.
The function given in the above code will sort the complete array by calling it recursively.
This function will operate on the given elements.
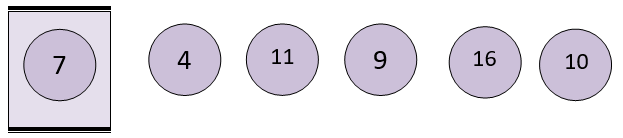
When the function name is called by the main section, the control goes to the function with the array and length of the array as first and second arguments.
Since the length of the array is not less than or equal to one the control does not enter the if condition and calls the function again with array as the first parameter and length-1 as the second parameter.
insertionSortRecursive(arr, 6-1)
insertionSortRecursive(arr, 5)
When the above function is called, it inserts the 6th node in the sorted array.
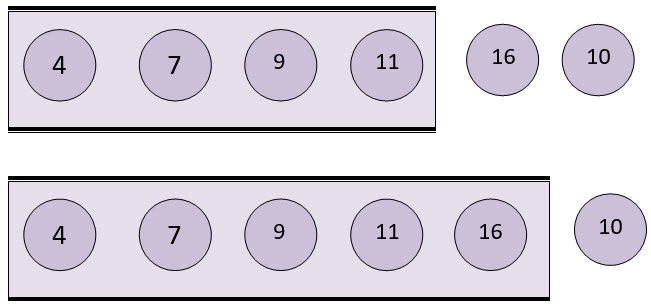
In the same way, the function is called multiple times with the same array but decreasing the length by 1 which looks something like this
insertionSortRecursive(arr,4)
This will insert the 5th node in the sorted array.
insertionSortRecursive(arr,3)
This will insert the 4th node in the sorted array.
insertionSortRecursive(arr,2)
This will insert the 3rd node in the sorted array.
insertionSortRecursive(arr,1)
This will insert the 2nd node in the sorted array.
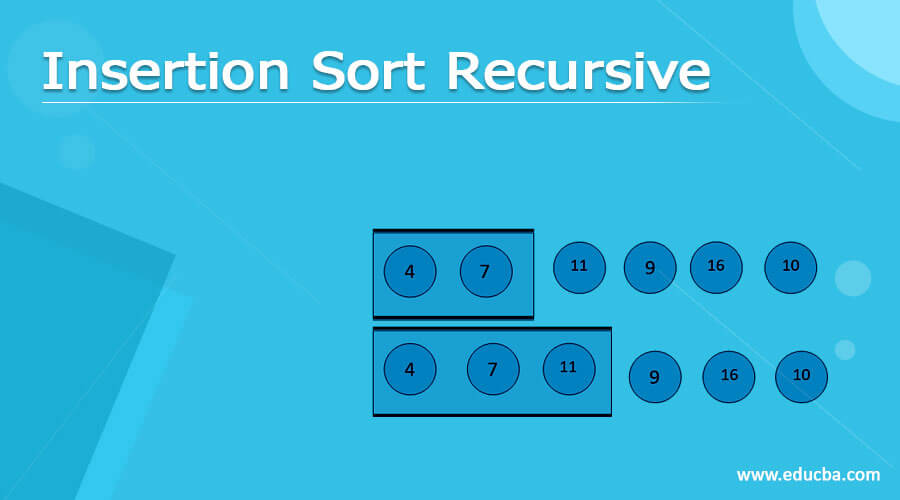
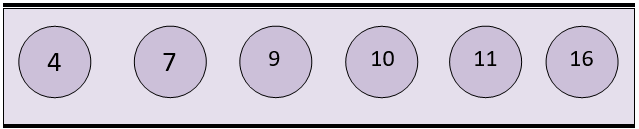
Now, a single element is left out in the array as shown below
Now we know that no more sorting is needed for a single element. So this acts as our base case to stop the recursive call. The array in the black box is sorted by the corresponding insertionSortRecursive() function as shown below.
The final array after sorting the elements is.
Complexity Analysis of Insertion Sort
Worst Case Complexity
Suppose, you have taken an array in descending order and you want to sort the elements in ascending order, In this case, the worst-case time complexity occurs.
Each element in the array must be compared with other elements which takes lots of time and ultimately, the n-1 number of comparisons occurs.
Thus, the total number of comparisons becomes n*(n-1) ~ n2, and the worst-time complexity is denoted as O(n2)
Best Case Complexity
When you consider an array that is already sorted, In that case, the algorithm requires minimum time to perform the sorting operation because the loop runs for n time and the inner loop does not run at all. So, there will be a linear complexity which is also known as best-case complexity as O(n).
Average Case Complexity
This case occurs when the elements in the array are in jumbled order (elements will be in neither descending nor ascending order). In that case, Average time complexity occurs as O(n2).
Space Complexity
The Space complexity of Insertion sort will be O(1) since an extra variable last is used.
Conclusion
Insertion Sort is an easy and one of the efficient sorting techniques that work the same way as you sort a pack of cards in your hand.• In this sorting technique, the array is divided into two parts that are, an unsorted array and a sorted one.
In Insertion Sort, a number is compared to another number then shifted to the correct place where it needs to be, and all the other elements are sorted in the same way. The Best case, Worst case, and Average case time complexities are O(n), O(n2), O(n2). The Space Complexity is O(1).
Recommended Articles
This is a guide to Insertion Sort Recursive. Here we discuss Introduction, concept, insert sort algorithm, and Complexity Analysis of Insertion Sort. You may also look at the following articles to learn more –